题目内容
【题目】某市为了了解高二学生物理学习情况，在34所高中里选出5所学校，随机抽取了近千名学生参加物理考试，将所得数据整理后，绘制出频率分布直方图如图所示．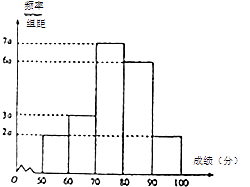 
（1）将34所高中随机编号为01，02，…，34，用下面的随机数表选取5组数抽取参加考试的五所学校，选取方法是从随机数表第一行的第6列和第7列数字开始，由左到右依次选取两个数字，则选出来的第4所学校的编号是多少？
49 54 43 54 82 17 37 93 23 78 87 35 20
96 43 84 26 34 91 64 57 24 55 06 88 77
04 74 47 67 21 76 33 50 25 83 92 12 06
（2）求频率分布直方图中a的值，试估计全市学生参加物理考试的平均成绩；
（3）如果从参加本次考试的同学中随机选取3名同学，这3名同学中考试成绩在80分以上，（含80分）的人数记为X，求X的分布列及数学期望．（注：频率可以视为相应的概率）
【答案】
（1）解：将34所高中随机编号为01，02，…，34，
用题中所给随机数表选取5组数抽取参加考试的五所学校，选取方法是从随机数表第一行的第6列和第7列数字开始，
由左到右依次选取两个数字，则选出来的五所学校依次为：21，32，09，16，17．
∴第4所学校的编号是16．
（2）解：由频率分布直方图的性质得：
2a+2a+3a+6a+7a=20a，20a×10=1，
解得a=0.005，
估计全市学生参加物理考试的平均成绩为：
0.1×55+0.15×65+0.35×75+03×85+0.1×95=76.5
（3）解：从参加考试的同学中随机抽取1名同学的成绩在80分以上的概率为 
X可能的取值是0，1，2，3
P（X=0）= 
，
P（X=1）= 
，
P（X=2）= 
，
P（X=3）= 
，
∴X的分布列为：
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
所以E（X）=0× 
（或X～B（3， ），所以E（X）=np=3× = 
）．
【解析】（1）由已知条件利用随机数法能求出第4所学校的编号．（2）由频率分布直方图的性质得2a+2a+3a+6a+7a=20a，由此能求出a=0.005，从而能估计全市学生参加物理考试的平均成绩．（3）从参加考试的同学中随机抽取1名同学的成绩在80分以上的概率为 ，X可能的取值是0，1，2，3，分别求出相应的概率，由此能求出X的分布列及数学期望．
【考点精析】通过灵活运用频率分布直方图和离散型随机变量及其分布列，掌握频率分布表和频率分布直方图，是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式，可展示数据的分布情况.通过作图既可以从数据中提取信息，又可以利用图形传递信息；在射击、产品检验等例子中，对于随机变量X可能取的值，我们可以按一定次序一一列出，这样的随机变量叫做离散型随机变量．离散型随机变量的分布列：一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn，X取每一个值 xi(i=1,2,......）的概率P(ξ=xi）＝Pi，则称表为离散型随机变量X 的概率分布，简称分布列即可以解答此题．
