[题目]已知在平面直角坐标系中的一个椭圆.它的中心在原点.左焦点为,右顶点为,设点．(1)求该椭圆的标准方程,(2)若是椭圆上的动点.求线段中点的轨迹方程, 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】已知在平面直角坐标系中的一个椭圆，它的中心在原点，左焦点为,右顶点为,设点．

（1）求该椭圆的标准方程；

（2）若是椭圆上的动点，求线段中点的轨迹方程；

【答案】（1）（2）

【解析】试题分析：（1）由左焦点为，右顶点为D（2，0），得到椭圆的半长轴a，半焦距c，再求得半短轴b，最后由椭圆的焦点在x轴上求得方程；（2）首先设所求点为M（x,y），借助于中点性质得到P点坐标用x,y表示，将P点代入椭圆方程从而得到中点的轨迹方程

试题解析：（1）由已知得椭圆的半长轴a=2,半焦距c=,则半短轴b=1．

又椭圆的焦点在x轴上, ∴椭圆的标准方程为

（2）设线段PA的中点为M（x,y）,点P的坐标是（x0,y0）,

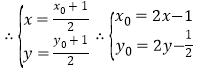
由点P在椭圆上,得,

∴线段PA中点M的轨迹方程是

练习册系列答案

相关题目

【题目】已知椭圆C的中心在原点，焦点在x轴上，左、右焦点分别为F1，F2，且|F1F2|=2，点（1，）在椭圆C上。

（1）求椭圆C的方程；

（2）过F1的直线l与椭圆C相交于A，B两点，且△AF2B的面积为，求以F2为圆心且与直线l相切的圆的方程。

【题目】在平面直角坐标系xOy中，已知P点到两定点D（﹣2，0），E（2，0）连线斜率之积为- ．
（1）求证：动点P恒在一个定椭圆C上运动；
（2）过的直线交椭圆C于A，B两点，过O的直线交椭圆C于M，N两点，若直线AB与直线MN斜率之和为零，求证：直线AM与直线BN斜率之和为定值．

【题目】已知函数．

（1）求函数在处的切线方程；

（2）设，讨论函数的零点个数．

【题目】如图，在四棱锥中，，．

（1）求证：；

（2）试在线段上找一点，使平面，并说明理由．

【题目】海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比，收获时各随机抽取了100个网箱，测量各箱水产品的产量（单位：kg）, 其频率分布直方图如下：

（1）记A表示事件“旧养殖法的箱产量低于50 kg”，估计A的概率；

（2）填写下面列联表，并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关：

	箱产量＜50 kg	箱产量≥50 kg
旧养殖法
新养殖法

（3）根据箱产量的频率分布直方图，对这两种养殖方法的优劣进行比较.

附：

P（）	0.050 0.010 0.001
k	3.841 6.635 10.828

【题目】设有关于x的一元二次方程x2+2ax+b2=0.

(1)若a是从0,1,2,3四个数中任取的一个数,b是从0,1,2三个数中任取的一个数,求上述方程有实根的概率.

(2)若a是从区间[0,3]任取的一个数,b是从区间[0,2]任取的一个数,求上述方程有实根的概率.

【题目】如图，在多面体ABCDE中，DB⊥平面ABC，AE∥DB，且△ABC为等边三角形，AE=1，BD=2，CD与平面ABCDE所成角的正弦值为．

（1）若F是线段CD的中点，证明：EF⊥平面DBC；
（2）求二面角D﹣EC﹣B的平面角的余弦值．

【题目】已知函数是奇函数，

（1）求实数m的值；

（2）判断函数的单调性并用定义法加以证明；

（3）若函数在上的最小值为，求实数a的值．

试题分类