题目内容
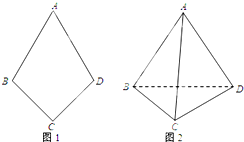 如图1,平面四边形ABCD关于直线AC对称,∠A=60°,∠C=
如图1,平面四边形ABCD关于直线AC对称,∠A=60°,∠C=90°,CD=2,把△ABD沿BD折起(如图2),使二面角A-BD-C为直二面角.如图2,
(Ⅰ)求AD与平面ABC所成的角的余弦值;
(Ⅱ)求二面角B-AC-D的大小的正弦值.
考点:二面角的平面角及求法,直线与平面所成的角
专题:综合题,空间位置关系与距离,空间角
分析:(Ⅰ)以BD的中点O为原点,OC所在的直线为x轴,OD所在的直线为y轴,OA所在的直线为z轴建立空间直角坐标系,求出面ABC的法向量,利用向量的夹角公式求AD与平面ABC所成的角的余弦值;
(Ⅱ)求得面ACD的法向量,利用向量的夹角公式求二面角B-AC-D的大小的正弦值.
(Ⅱ)求得面ACD的法向量,利用向量的夹角公式求二面角B-AC-D的大小的正弦值.
解答:
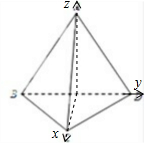 解:如图所示,以BD的中点O为原点,OC所在的直线为x轴,OD所在的直线为y轴,OA所在的直线为z轴建立空间直角坐标系,则O(0,0,0),D(0,
解:如图所示,以BD的中点O为原点,OC所在的直线为x轴,OD所在的直线为y轴,OA所在的直线为z轴建立空间直角坐标系,则O(0,0,0),D(0,
,0),B(0,-
,0),C(
,0,0),A(0,0,
)
(Ⅰ)设面ABC的法向量为
=(x,y,z),
∵
=(0,-
,-
),
=(
,
,0)
∴由
,可得
,
取z=1有
=(
,-
,1)
∵
=(0,
,-
),
∴cos?
,
>=-
,
∴AD与面ABC所成角的余弦值是
.…(6分)
(Ⅱ)同理求得面ACD的法向量为
=(
,
,1),则cos?
,
>=
则二面角B-AC-D的正弦值为
.…(12分)
 解:如图所示,以BD的中点O为原点,OC所在的直线为x轴,OD所在的直线为y轴,OA所在的直线为z轴建立空间直角坐标系,则O(0,0,0),D(0,
解:如图所示,以BD的中点O为原点,OC所在的直线为x轴,OD所在的直线为y轴,OA所在的直线为z轴建立空间直角坐标系,则O(0,0,0),D(0,| 2 |
| 2 |
| 2 |
| 6 |
(Ⅰ)设面ABC的法向量为
| n |
∵
| AB |
| 2 |
| 6 |
| BC |
| 2 |
| 2 |
∴由
|
|
取z=1有
| n |
| 3 |
| 3 |
∵
| AD |
| 2 |
| 6 |
∴cos?
| AD |
| n |
| ||
| 7 |
∴AD与面ABC所成角的余弦值是
2
| ||
| 7 |
(Ⅱ)同理求得面ACD的法向量为
| n1 |
| 3 |
| 3 |
| n |
| n1 |
| 1 |
| 7 |
则二面角B-AC-D的正弦值为
4
| ||
| 7 |
点评:本题考查二面角、线面角的求法,考查用向量解决立体几何问题的方法能力,考查数形结合、空间想象能力,属于中档题.

练习册系列答案
相关题目
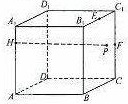 如图,已知正方体ABCD-A1B1C1D1的棱长为4,点H在棱AA1上,且HA1=1,点E、F分别为B1C1、CC1的中点,P为侧面BCC1B1上一动点,且PE⊥PF,则当点P运动时,求HP2的最小值是( )
如图,已知正方体ABCD-A1B1C1D1的棱长为4,点H在棱AA1上,且HA1=1,点E、F分别为B1C1、CC1的中点,P为侧面BCC1B1上一动点,且PE⊥PF,则当点P运动时,求HP2的最小值是( )| A、9 | ||
B、27--6
| ||
C、51-14
| ||
D、14-3
|