题目内容
已知圆锥曲线E:
+
=c2+1(c>0,c≠1)的离心率为e=
,过原点O的直线与曲线E交于P、A两点,其中P在第一象限,B是曲线E上不同于P、A的点,直线PB、AB的斜率分别为k1、k2,且k1k2≠0.
(Ⅰ)求圆锥曲线E的标准方程;
(Ⅱ)求k1•k2的值;
(Ⅲ)已知F为圆锥曲线E的右焦点,若PA⊥PB,且存在λ∈R使
=λ
,求直线AB的方程.
| (x-c)2+y2 |
| (x+c)2+y2 |
| ||
| 2 |
(Ⅰ)求圆锥曲线E的标准方程;
(Ⅱ)求k1•k2的值;
(Ⅲ)已知F为圆锥曲线E的右焦点,若PA⊥PB,且存在λ∈R使
| AF |
| BF |
考点:轨迹方程,直线与圆锥曲线的关系
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)首先,设点F1(-c,0),F2(c,0),M(x,y),然后,结合给定的条件,得到|MF1|+|MF2|=c2+1>|F1F2|=2c,从而,得到其轨迹是一个椭圆,然后利用待定系数法确定其方程;
(Ⅱ)首先,可以设点P(x0,y0),根据椭圆的对称性,得点A(-x0,-y0),点B(x1,y1),然后,根据椭圆的标准方程和斜率公式进行化简求解;
(Ⅲ)根据(Ⅰ)得F(
,0),设直线PB的斜率为k,k<0,得到直线PA的斜率为-
,直线AB的斜率为-
,直线PA的方程为:y=-
x,直线AB的方程为:y=-
(x-
),然后,利用直线与椭圆相交,求点A坐标,再借助于斜率公式建立等式,求解斜率k的值,然后,写出直线AB的方程即可.
(Ⅱ)首先,可以设点P(x0,y0),根据椭圆的对称性,得点A(-x0,-y0),点B(x1,y1),然后,根据椭圆的标准方程和斜率公式进行化简求解;
(Ⅲ)根据(Ⅰ)得F(
3
| ||
| 5 |
| 1 |
| k |
| 1 |
| 4k |
| 1 |
| k |
| 1 |
| 4k |
3
| ||
| 5 |
解答:
解:(Ⅰ)设点F1(-c,0),F2(c,0),M(x,y),
∵
+
=c2+1(c>0,c≠1),
∴|MF1|+|MF2|=c2+1>|F1F2|=2c,
∴点M的轨迹是一个以F1(-c,0),F2(c,0)为焦点的椭圆,
设其方程为
+
=1,(a>b>0),
∴2a=c2+1,①
∵e=
=
,
∴c=
a ②,
根据①②得,
a=2,c=
,或a=
,c=
;
∴b2=a2-c2=1或b2=a2-c2=
,
∴b=1或
∴曲线E的标准方程:
+y2=1或
+
=1;
(Ⅱ)设点P(x0,y0),根据椭圆的对称性,得点A(-x0,-y0),
设点B(x1,y1),则y02=1-
x02,y12=1-
x12,
k1=
,
k2=
,
∴k1•k2=
,
=
,
=-
,
∴k1•k2=-
.
(Ⅲ)由已知设P(m,n),又由A、P关于原点对称,则A的坐标为(-m,-n);
当E的方程为
+y2=1时,
F(
,0),k2=
,k1=-
;
∵PA⊥PB,(
)•
=-1,得m=
;
易得n=
,k2=
,
AB所在直线的方程为y=
(x-
),
同理,当E的方程为
+
=1;可得AB所在直线的方程为y=
(x-
),
故AB所在直线的方程为y=
(x-
).
∵
| (x-c)2+y2 |
| (x+c)2+y2 |
∴|MF1|+|MF2|=c2+1>|F1F2|=2c,
∴点M的轨迹是一个以F1(-c,0),F2(c,0)为焦点的椭圆,
设其方程为
| x2 |
| a2 |
| y2 |
| b2 |
∴2a=c2+1,①
∵e=
| c |
| a |
| ||
| 2 |
∴c=
| ||
| 2 |
根据①②得,
a=2,c=
| 3 |
| 2 |
| 3 |
| ||
| 3 |
∴b2=a2-c2=1或b2=a2-c2=
| 1 |
| 9 |
∴b=1或
| 1 |
| 3 |
∴曲线E的标准方程:
| x2 |
| 4 |
| x2 | ||
|
| y2 | ||
|
(Ⅱ)设点P(x0,y0),根据椭圆的对称性,得点A(-x0,-y0),
设点B(x1,y1),则y02=1-
| 1 |
| 4 |
| 1 |
| 4 |
k1=
| y1-y0 |
| x1-x0 |
k2=
| y1+y0 |
| x1+x0 |
∴k1•k2=
| y12-y02 |
| x12-x02 |
=
-
| ||
| x12-x02 |
=-
| 1 |
| 4 |
∴k1•k2=-
| 1 |
| 4 |
(Ⅲ)由已知设P(m,n),又由A、P关于原点对称,则A的坐标为(-m,-n);
当E的方程为
| x2 |
| 4 |
F(
| 3 |
| n | ||
|
| ||
| n |
∵PA⊥PB,(
| ||
| n |
| n |
| m |
| ||
| 3 |
易得n=
| ||
| 6 |
| ||
| 8 |
AB所在直线的方程为y=
| ||
| 8 |
| 3 |
同理,当E的方程为
| x2 | ||
|
| y2 | ||
|
| ||
| 8 |
| 3 |
故AB所在直线的方程为y=
| ||
| 8 |
| 3 |
点评:本题重点考查了椭圆的概念、标准方程、椭圆的几何性质和直线与椭圆的位置关系、平面向量等知识,属于综合性题目,难度中等,属于中档题.

练习册系列答案
相关题目
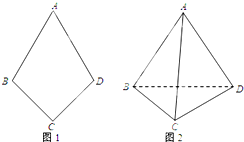 如图1,平面四边形ABCD关于直线AC对称,∠A=60°,∠C=
如图1,平面四边形ABCD关于直线AC对称,∠A=60°,∠C=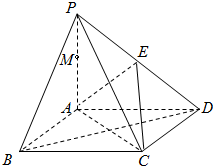 如图,棱锥P-ABCD的底面ABCD是矩形,PA⊥面ABCD,PA=AD=4,BD=4
如图,棱锥P-ABCD的底面ABCD是矩形,PA⊥面ABCD,PA=AD=4,BD=4