题目内容
已知椭圆C:
+
=1(a>b>0)的左焦点为A,上顶点为B,左焦点为F,且∠AFB=150°,△AFB=150°,△AFB的面积为1-
,求此椭圆方程.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
考点:椭圆的简单性质
专题:计算题,作图题,圆锥曲线的定义、性质与方程
分析:由题意作图,由∠AFB=150°可得a=2b,c=
b,再由三角形面积可求出椭圆的方程.
| 3 |
解答:
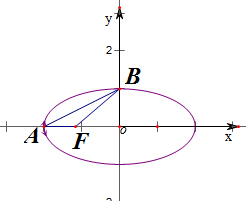 解:如图,∵∠AFB=150°,
解:如图,∵∠AFB=150°,
∴∠BFO=30°,
故a=2b,c=
b;
又∵△AFB的面积为1-
,
∴
(a-c)b=1-
,
即(2b-
b)b=2-
,
解得,b=1;
故椭圆方程为:
+y2=1.
 解:如图,∵∠AFB=150°,
解:如图,∵∠AFB=150°,∴∠BFO=30°,
故a=2b,c=
| 3 |
又∵△AFB的面积为1-
| ||
| 2 |
∴
| 1 |
| 2 |
| ||
| 2 |
即(2b-
| 3 |
| 3 |
解得,b=1;
故椭圆方程为:
| x2 |
| 4 |
点评:本题考查了椭圆的方程的求法,属于基础题.

练习册系列答案
相关题目
设非空集合A⊆{1,2,3,4,5},且若a∈A,则6-a∈A,这样的集合共有( )个.
| A、5 | B、6 | C、7 | D、8 |
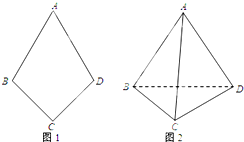 如图1,平面四边形ABCD关于直线AC对称,∠A=60°,∠C=
如图1,平面四边形ABCD关于直线AC对称,∠A=60°,∠C=