题目内容
已知结论:“在正三角形ABC中,若D是边BC的中点,G是三角形ABC的重心,则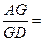

 2”。若把该结论推广到空间,则有结论:“在棱长都相等的四面体
2”。若把该结论推广到空间,则有结论:“在棱长都相等的四面体 中,若
中,若 的中心为
的中心为 ,四面体内部一点
,四面体内部一点 到四面体各面的距离都相等,则
到四面体各面的距离都相等,则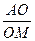 = 。
= 。
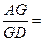

 2”。若把该结论推广到空间,则有结论:“在棱长都相等的四面体
2”。若把该结论推广到空间,则有结论:“在棱长都相等的四面体 中,若
中,若 的中心为
的中心为 ,四面体内部一点
,四面体内部一点 到四面体各面的距离都相等,则
到四面体各面的距离都相等,则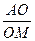 = 。
= 。3
略

练习册系列答案
相关题目
题目内容
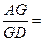

 2”。若把该结论推广到空间,则有结论:“在棱长都相等的四面体
2”。若把该结论推广到空间,则有结论:“在棱长都相等的四面体 中,若
中,若 的中心为
的中心为 ,四面体内部一点
,四面体内部一点 到四面体各面的距离都相等,则
到四面体各面的距离都相等,则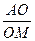 = 。
= 。