题目内容
如图所示几何体中,平面PAC⊥平面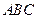 ,
,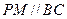 ,PA = PC,
,PA = PC,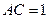 ,
,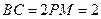 ,
,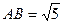 ,若该几何体左视图(侧视图)的面积为
,若该几何体左视图(侧视图)的面积为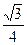 .
.
(1)求证:PA⊥BC;
(2)画出该几何体的主视图(正视图)并求其面积S;
(3)求出多面体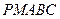 的体积V.
的体积V.
 ,
,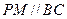 ,PA = PC,
,PA = PC,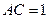 ,
,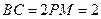 ,
,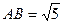 ,若该几何体左视图(侧视图)的面积为
,若该几何体左视图(侧视图)的面积为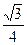 .
.(1)求证:PA⊥BC;
(2)画出该几何体的主视图(正视图)并求其面积S;
(3)求出多面体
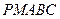 的体积V.
的体积V.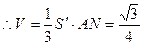
解:(1)
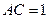 ,BC=2,
,BC=2,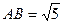 ,
,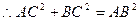 ,∴
,∴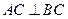 , …………2分
, …………2分∵平面PAC⊥平面
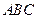 ,平面PAC∩平面
,平面PAC∩平面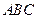 =AC,
=AC,∴BC⊥平面PAC
∵PA
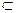 平面PAC, ∴PA⊥BC. …………4分
平面PAC, ∴PA⊥BC. …………4分(2)该几何体的主视图如下:
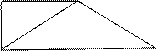 …………6分
…………6分∵PA = PC,取AC的中点D,连接PD,则PD⊥AC,
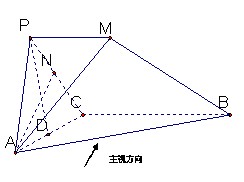
又平面PAC⊥平面
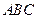 ,则PD⊥平面ABC,
,则PD⊥平面ABC,∴几何体左视图的面积=
 =
=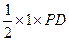 =
=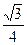 .
.∴PD=
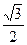 ,并易知
,并易知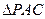 是边长为1的正三角形,…………8分
是边长为1的正三角形,…………8分∴主视图的面积是上、下底边长分别为1和2,PD的长为高的直角梯形的面积,
∴S=
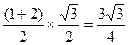 . …………10分
. …………10分(3)取PC的中点N,连接AN,由
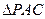 是边长为1的正三角形,可知AN⊥PC,
是边长为1的正三角形,可知AN⊥PC,由(1)BC⊥平面PAC,可知AN⊥BC,
∴AN⊥平面PCBM,
∴AN是四棱锥A—PCBM的高且AN=
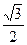 ,…………12分
,…………12分由BC⊥平面PAC,可知BC⊥PC,
由
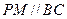 可知四边形PCBM是上、下底边长分别为1和2,PC的长1为高的
可知四边形PCBM是上、下底边长分别为1和2,PC的长1为高的直角梯形,其面积
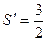 .
.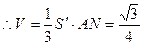 .…………14分
.…………14分
练习册系列答案
相关题目
 是一个长方体,
是一个长方体, 是一个四棱锥.
是一个四棱锥. ,
, ,点
,点 且
且 .
. ;
; 与面
与面 所成的角的正切值;
所成的角的正切值; ,当
,当 为何值时,
为何值时, .
.



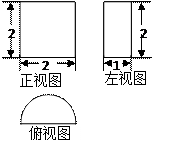

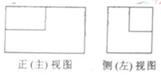
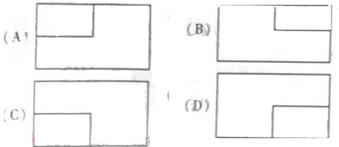
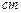 ), 则按图中尺寸,做成的工作台用去的合板的
), 则按图中尺寸,做成的工作台用去的合板的 。(制作过程合板损耗和合板厚度忽略不计)
。(制作过程合板损耗和合板厚度忽略不计)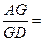

 2”。若把该结论推广到空间,则有结论:“在棱长都相等的四面体
2”。若把该结论推广到空间,则有结论:“在棱长都相等的四面体 中,若
中,若 的中心为
的中心为 ,四面体内部一点
,四面体内部一点 到四面体各面的距离都相等,则
到四面体各面的距离都相等,则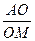 = 。
= 。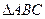 中,若
中,若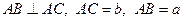 ,则
,则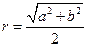 ,将此结论拓展到空间,可得出的正确结论是:在四面体
,将此结论拓展到空间,可得出的正确结论是:在四面体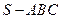 中,若
中,若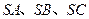 两两垂直,
两两垂直,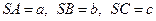 ,则四面体
,则四面体 .
.