题目内容
已知数列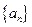 是等差数列,
是等差数列, 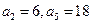 ;数列
;数列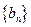 的前n项和是
的前n项和是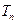 ,且
,且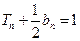 .
.
(Ⅰ) 求数列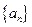 的通项公式;
的通项公式;
(Ⅱ) 求证:数列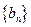 是等比数列;
是等比数列;
(Ⅲ) 记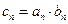 ,求
,求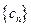 的前n项和
的前n项和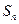 .
.
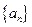 是等差数列,
是等差数列, 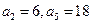 ;数列
;数列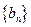 的前n项和是
的前n项和是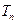 ,且
,且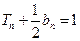 .
.(Ⅰ) 求数列
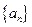 的通项公式;
的通项公式; (Ⅱ) 求证:数列
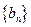 是等比数列;
是等比数列;(Ⅲ) 记
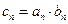 ,求
,求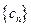 的前n项和
的前n项和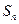 .
.(Ⅰ)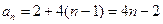 (Ⅱ)略(Ⅲ)
(Ⅱ)略(Ⅲ) 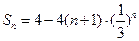
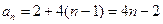 (Ⅱ)略(Ⅲ)
(Ⅱ)略(Ⅲ) 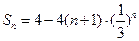
Ⅰ)设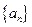 的公差为
的公差为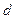 ,则:
,则: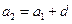 ,
,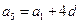 ,
,
∵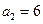 ,
,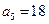 ,∴
,∴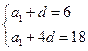 ,∴
,∴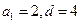 .
.
∴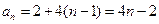 .
.
(Ⅱ)当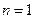 时,
时, ,由
,由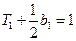 ,得
,得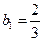 .
.
当 时,
时,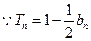 ,
,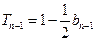 ,
,
∴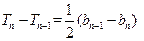 ,即
,即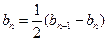 .
.
∴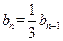 .
.
∴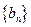 是以
是以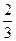 为首项,
为首项,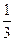 为公比的等比数列.
为公比的等比数列.
(Ⅲ)由(2)可知: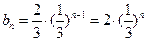 .
.
∴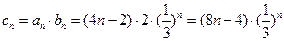 .
.
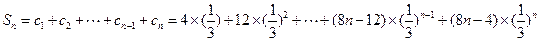 .
.
∴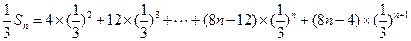 .
.
∴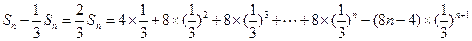

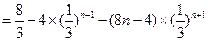 .
.
∴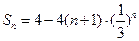 .
.
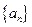 的公差为
的公差为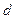 ,则:
,则: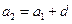 ,
,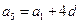 ,
,∵
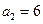 ,
,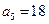 ,∴
,∴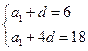 ,∴
,∴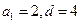 .
. ∴
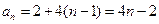 .
. (Ⅱ)当
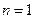 时,
时, ,由
,由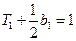 ,得
,得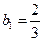 .
. 当
 时,
时,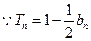 ,
,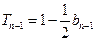 ,
,∴
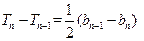 ,即
,即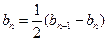 .
. ∴
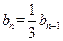 .
. ∴
 是以
是以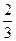 为首项,
为首项,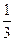 为公比的等比数列.
为公比的等比数列. (Ⅲ)由(2)可知:
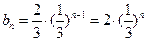 .
. ∴
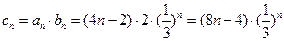 .
. 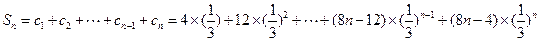 .
.∴
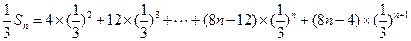 .
.∴
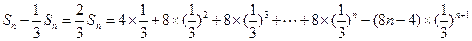

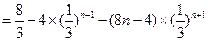 .
.∴
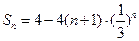 .
. 
练习册系列答案
相关题目
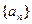 的通项公式为
的通项公式为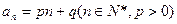 。数列
。数列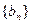 定义如下:对于正整数m,
定义如下:对于正整数m,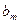 是使得不等式
是使得不等式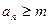 成立的所有n中的最小值。 (1)若
成立的所有n中的最小值。 (1)若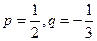 ,求b3; (2)若
,求b3; (2)若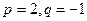 ,求数列
,求数列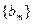 的前2m项和公式;(3)是否存在p和q,使得
的前2m项和公式;(3)是否存在p和q,使得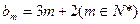 ?如果存在,求p和q的取值范围;如果不存在,请说明理由。
?如果存在,求p和q的取值范围;如果不存在,请说明理由。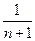 +
+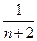 +
+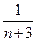 +……+
+……+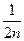 >a对于一切大于1的自然数n都成立,求实数a的取值范围。
>a对于一切大于1的自然数n都成立,求实数a的取值范围。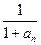 ,求a2008。
,求a2008。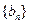 的前
的前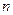 项和为
项和为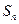 ,且
,且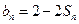 ;数列
;数列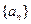 为等差数列,且
为等差数列,且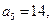
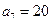 .
.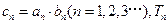 为数列
为数列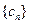 的前
的前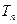 .
.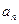 }的前n项和记为Sn.已知
}的前n项和记为Sn.已知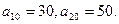 (Ⅰ)求通项
(Ⅰ)求通项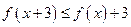 和
和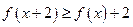 ,且
,且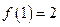 ,记
,记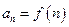
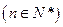 ,则
,则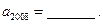

 中,
中, ,那么
,那么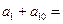 .
.