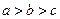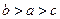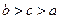题目内容
(本小题满分13分)已知函数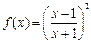 (其中x≥1)
(其中x≥1)
(1)求函数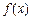 的反函数
的反函数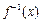 ;
;
(2)设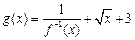 ,求函数
,求函数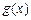 最小值及相应的x值;
最小值及相应的x值;
(3)若不等式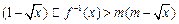 对于区间
对于区间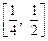 上的每一个x值都成立,求实数m的取值范围.
上的每一个x值都成立,求实数m的取值范围.
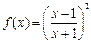 (其中x≥1)
(其中x≥1)(1)求函数
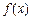 的反函数
的反函数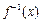 ;
;(2)设
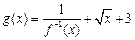 ,求函数
,求函数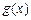 最小值及相应的x值;
最小值及相应的x值;(3)若不等式
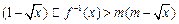 对于区间
对于区间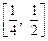 上的每一个x值都成立,求实数m的取值范围.
上的每一个x值都成立,求实数m的取值范围.(1)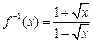
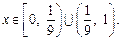
(2)即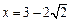 时,
时,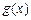 有最小值
有最小值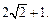 (3)
(3)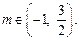
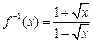
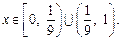
(2)即
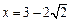 时,
时,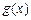 有最小值
有最小值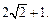 (3)
(3)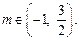
(1)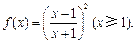
∵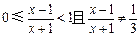 ,∴函数
,∴函数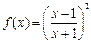 的值域为
的值域为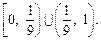
由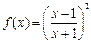 ,得
,得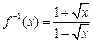 ,因此,函数
,因此,函数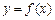 的反函数
的反函数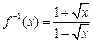
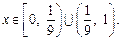
(2)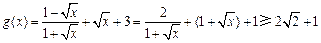 ,当且仅当
,当且仅当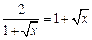 ,
,
即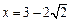 时,
时,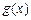 有最小值
有最小值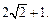
(3)由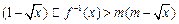 ,得
,得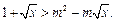
设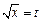 ,则
,则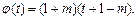
根据题意,对区间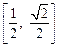 中的一切t值,
中的一切t值,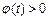 恒成立.
恒成立.
则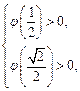 得
得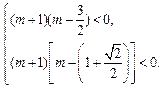 ∴
∴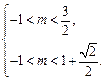
∴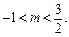 即实数m的取值范围是
即实数m的取值范围是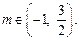
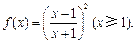
∵
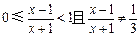 ,∴函数
,∴函数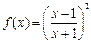 的值域为
的值域为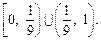
由
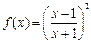 ,得
,得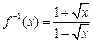 ,因此,函数
,因此,函数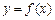 的反函数
的反函数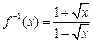
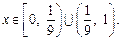
(2)
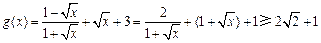 ,当且仅当
,当且仅当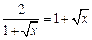 ,
,即
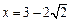 时,
时,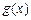 有最小值
有最小值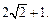
(3)由
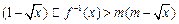 ,得
,得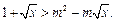
设
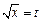 ,则
,则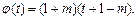
根据题意,对区间
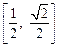 中的一切t值,
中的一切t值,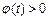 恒成立.
恒成立.则
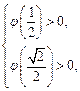 得
得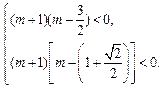 ∴
∴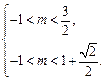
∴
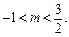 即实数m的取值范围是
即实数m的取值范围是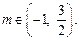

练习册系列答案
相关题目
 上的函数
上的函数 满足
满足 ,若
,若 ,则
,则 ( )
( )



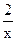 的值域为[3,9],K
的值域为[3,9],K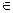 [3,9]时,f(x)=K有两不等的根x1,x2,求x1+x2.
[3,9]时,f(x)=K有两不等的根x1,x2,求x1+x2.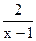 的值域为[7,11],K
的值域为[7,11],K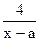 -b , x>a
-b , x>a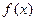 是周期为2的奇函数,当
是周期为2的奇函数,当 时,
时,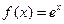 则
则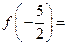
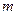 人,每人每年可创利100千元.据测算,若裁员人数不超过现有人数的20%,则每裁员1人,留岗员工每人每年就能多创利1千元;若裁员人数超过现有人数的20%,则每裁员1人,留岗员工每人每年就能多创利2千元.为保证公司的正常运转,留岗的员工数不得少于现有员工人数的75%.为保障被裁员工的生活,公司要付给被裁员工每人每年20千元的生活费.
人,每人每年可创利100千元.据测算,若裁员人数不超过现有人数的20%,则每裁员1人,留岗员工每人每年就能多创利1千元;若裁员人数超过现有人数的20%,则每裁员1人,留岗员工每人每年就能多创利2千元.为保证公司的正常运转,留岗的员工数不得少于现有员工人数的75%.为保障被裁员工的生活,公司要付给被裁员工每人每年20千元的生活费.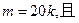 15<
15<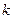 <50,为了获得最大的经济效益,该公司应裁员多少人?
<50,为了获得最大的经济效益,该公司应裁员多少人?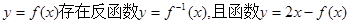 的图象过点(2,1),则函数
的图象过点(2,1),则函数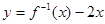 的图象一定过点( )
的图象一定过点( )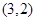
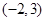
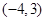
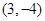
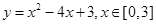 的值域为( )
的值域为( )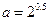 ,
,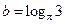 ,
, ,则( )
,则( )