题目内容
由等式x4+a1x3+a2x2+a3x+a4=(x+1)4+b1(x+1)3+b2(x+1)2+b3(x+1)+b4,定义映射f:(a1,a2,a3,a4)→(b1,b2,b3,b4),则f(4,3,2,1)等于( )
| A.(1,2,3,4) | B.(0,3,4,0) | C.(-1,0,2,-2) | D.(0,-3,4,-1) |
比较等式两边x3的系数,得4=4+b1,则b1=0,故排除A,C;
再比较等式两边的常数项,有1=1+b1+b2+b3+b4,
∴b1+b2+b3+b4=0.故排除B
故应选D.
再比较等式两边的常数项,有1=1+b1+b2+b3+b4,
∴b1+b2+b3+b4=0.故排除B
故应选D.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
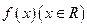 满足
满足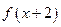 =
=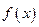 ,且
,且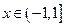 时,
时,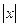 ,则函数
,则函数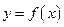 的图像与函数
的图像与函数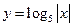 的图像交点个数是
的图像交点个数是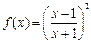 (其中x≥1)
(其中x≥1)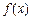 的反函数
的反函数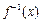 ;
;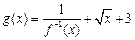 ,求函数
,求函数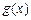 最小值及相应的x值;
最小值及相应的x值;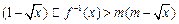 对于区间
对于区间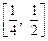 上的每一个x值都成立,求实数m的取值范围.
上的每一个x值都成立,求实数m的取值范围.
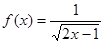 的定义域是 .
的定义域是 . 的定义域是 ( )
的定义域是 ( )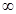 ,-1)
,-1)