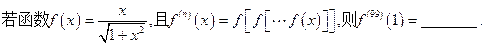题目内容
(1)f(x)="x" + 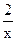 的值域为[3,9],K
的值域为[3,9],K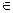 [3,9]时,f(x)=K有两不等的根x1,x2,求x1+x2.
[3,9]时,f(x)=K有两不等的根x1,x2,求x1+x2.
(2)g (x) =x+2+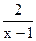 的值域为[7,11],K
的值域为[7,11],K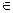 [7,11]时,g(x)=K
[7,11]时,g(x)=K
也有两不等根x3、x4,求x3+x4
(3)h(x) =x+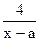 -b , x>a
-b , x>a
h(x)=K的两根之和为K+18,且h(x)的最小值为0,试求a与b的值。
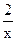 的值域为[3,9],K
的值域为[3,9],K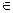 [3,9]时,f(x)=K有两不等的根x1,x2,求x1+x2.
[3,9]时,f(x)=K有两不等的根x1,x2,求x1+x2.(2)g (x) =x+2+
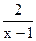 的值域为[7,11],K
的值域为[7,11],K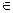 [7,11]时,g(x)=K
[7,11]时,g(x)=K也有两不等根x3、x4,求x3+x4
(3)h(x) =x+
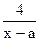 -b , x>a
-b , x>ah(x)=K的两根之和为K+18,且h(x)的最小值为0,试求a与b的值。
(1)x1+x2="K " (2)x3+x4=k-1 (3) a="7 " b=11
(1)∵x+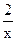 ≥3 K=x+
≥3 K=x+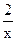
∴x>0 x2-kx+2=0
△ =k2-8≥1
∴ x1+ x2=K
即x1+x2=K
(2)∵K=x+2+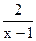
∴ (x-1)2-(K-3)(x-1) =0
△ = (K-3)2≥8
∴(x3-1)+(x4-1)=K-3
∴ x3+ x4=K-1
即x3+x4=k-1
(3)设h(x)=k的两根为x5,x6,则x5+x6=k+18
∵h(x)=(x-a)+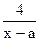 +(a-b)
+(a-b)
≥a-b+4 ①
由k(x-a)+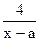 +(a-b)得
+(a-b)得
k-(a-b) = (x5-a)+(x6-a)
=k+18-2a
∴a+b-18="0 " ②
 联立①②得 a=7
联立①②得 a=7
b=11
即:a、b的值为7和11。
考察考生联想、类比、递推的能力,函数与方程的综合应用能力。
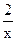 ≥3 K=x+
≥3 K=x+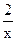
∴x>0 x2-kx+2=0
△ =k2-8≥1
∴ x1+ x2=K
即x1+x2=K
(2)∵K=x+2+
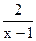
∴ (x-1)2-(K-3)(x-1) =0
△ = (K-3)2≥8
∴(x3-1)+(x4-1)=K-3
∴ x3+ x4=K-1
即x3+x4=k-1
(3)设h(x)=k的两根为x5,x6,则x5+x6=k+18
∵h(x)=(x-a)+
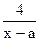 +(a-b)
+(a-b)≥a-b+4 ①
由k(x-a)+
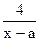 +(a-b)得
+(a-b)得k-(a-b) = (x5-a)+(x6-a)
=k+18-2a
∴a+b-18="0 " ②
 联立①②得 a=7
联立①②得 a=7b=11
即:a、b的值为7和11。
考察考生联想、类比、递推的能力,函数与方程的综合应用能力。

练习册系列答案
相关题目
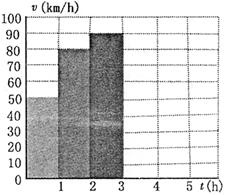
 m,试将汽车行驶这段路程时汽车里程表读数S表示为时间t的函数。
m,试将汽车行驶这段路程时汽车里程表读数S表示为时间t的函数。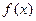 满足:x≥4,则
满足:x≥4,则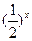 ;当x<4时
;当x<4时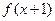 ,则
,则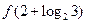 =( )
=( )
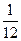
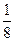
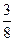
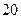 m/s.一列有55辆车身长都为10m的同一车型的车队(这种型号的车能行驶的最高速为40m/s),匀速通过该隧道,设车队的速度为
m/s.一列有55辆车身长都为10m的同一车型的车队(这种型号的车能行驶的最高速为40m/s),匀速通过该隧道,设车队的速度为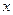 m/s ,根据安全和车流的需要,当
m/s ,根据安全和车流的需要,当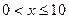 时,相邻两车之间保持20 m的距离;当
时,相邻两车之间保持20 m的距离;当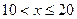 时,相邻两车之间保持
时,相邻两车之间保持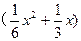 m的距离.自第1辆车车头进入隧道至第55辆车尾离开隧道所用的时间为
m的距离.自第1辆车车头进入隧道至第55辆车尾离开隧道所用的时间为 . (I)将
. (I)将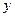 表示为
表示为 函数;(II)求车队通过隧道时间
函数;(II)求车队通过隧道时间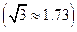
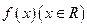 满足
满足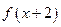 =
=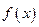 ,且
,且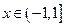 时,
时,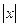 ,则函数
,则函数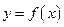 的图像与函数
的图像与函数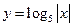 的图像交点个数是
的图像交点个数是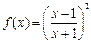 (其中x≥1)
(其中x≥1)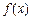 的反函数
的反函数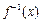 ;
;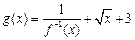 ,求函数
,求函数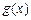 最小值及相应的x值;
最小值及相应的x值;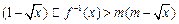 对于区间
对于区间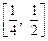 上的每一个x值都成立,求实数m的取值范围.
上的每一个x值都成立,求实数m的取值范围. 满足
满足 则
则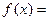
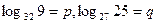 ,试用p,q表示lg5.
,试用p,q表示lg5.