题目内容
2.设(x3-1)(x+1)7=a0+a1(x+3)+a2(x+3)2…+a10(x+3)10,则a0+a1+a2+…+a10=9.分析 观察所给的等式,令x=-2,可以求出a0+a1+a2+…+a9+a10的值.
解答 解:∵(x3-1)(x+1)7=a0+a1(x+3)+a2(x+3)2…+a10(x+3)10,
令x=-2,则[(-2)3-1](-2+1)=a0+a1+a2+…+a9+a10,
∴a0+a1+a2+…+a10=(-9)×(-1)=9.
故答案为:9.
点评 本题考查了二项式定理的应用问题,解题时应根据题目的特点,利用特殊值代入法求出结果,是基础题目.

练习册系列答案
相关题目
12.两个变量y与x的回归模型中,分别选择了4个不同模型,它们的相关系数r如下,其中拟合效果最好的模型是( )
| 模型 | 模型1 | 模型2 | 模型3 | 模型4 |
| 相关系数r | 0.98 | 0.80 | 0.50 | 0.25 |
| A. | 模型1 | B. | 模型2 | C. | 模型3 | D. | 模型4 |
13.存在正实数b使得关于x的方程$sinx+\sqrt{3}cosx=b$的正根从小到大排成一个等差数列,若点 P(6,b)在直线mx+ny-2=0上(m,n均为正常数),则$\frac{1}{m}+\frac{4}{n}$的最小值为( )
| A. | $5+2\sqrt{6}$ | B. | $4\sqrt{3}$ | C. | $8\sqrt{3}$ | D. | $7+4\sqrt{3}$ |
11.与直线4x-3y+5=0关于x轴对称的直线方程为( )
| A. | 4x+3y+5=0 | B. | 4x-3y+5=0 | C. | 4x+3y-5=0 | D. | 4x-3y-5=0 |
12.某产品的广告费用x(万元)与销售额y(万元)的统计数据如表,根据右表可得回归方程$\hat y=\hat bx+\hat a$中的$\hat a=0$,据此模型预报广告费用为6万元时销售额为( )
| x | 4 | 2 | 3 | 5 |
| y | 38 | 20 | 31 | 51 |
| A. | 50 | B. | 60 | C. | 63 | D. | 59 |
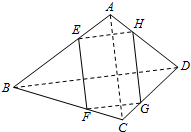 如图所示,ABCD是空间四边形,E、F、G、H分别是四边上的点,并且AC∥面EFGH,BD∥面EFGH,AC=2,BD=4,当EFGH是菱形时,$\frac{AE}{EB}$的值是$\frac{AE}{EB}$.
如图所示,ABCD是空间四边形,E、F、G、H分别是四边上的点,并且AC∥面EFGH,BD∥面EFGH,AC=2,BD=4,当EFGH是菱形时,$\frac{AE}{EB}$的值是$\frac{AE}{EB}$.