题目内容
10.在平面斜坐标系xOy中,∠xOy=60°,平面上任意一点P关于斜坐标系xOy的斜坐标定义为:若$\overrightarrow{OP}$=x$\overrightarrow{{e}_{1}}$+y$\overrightarrow{{e}_{2}}$$\overrightarrow{OP}=x\overrightarrow{e_1}+y\overrightarrow{e_2}$,其中向量$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$分别为斜坐标轴x,y轴同方向的单位向量,则P点的坐标为(x,y).(1)若P点的坐标为(3,-2),则|$\overrightarrow{OP}$|$\sqrt{7}$;
(2)以O为圆心,2为半径的圆在斜坐标系下的方程为x2+y2+xy=4.
分析 (1)若P点的坐标为(3,-2),利用数量积得性质可得|$\overrightarrow{OP}$|;
(2)以O为圆心,2为半径的圆满足|$\overrightarrow{OP}$|=1,利用数量积得性质即可得出结论.
解答 解:(1)∵$\overrightarrow{OP}=3\overrightarrow{e_1}-2\overrightarrow{e_2}$,
∴$|\overrightarrow{OP}{|^2}=9\overrightarrow e_1^2-2×3×2{\overrightarrow e_1}•{\overrightarrow e_2}+4\overrightarrow e_2^2$=$9-2×2×3|{\overrightarrow e_1}|•|{\overrightarrow e_2}|cos{60°}+4$=7,
故$|\overrightarrow{OP}|=\sqrt{7}$.
(2)∵$|\overrightarrow{OP}|=|x\overrightarrow{e_1}+y\overrightarrow{e_2}|=2$,∴$|\overrightarrow{OP}{|^2}={x^2}\overrightarrow e_1^2+2xy{\overrightarrow e_1}•{\overrightarrow e_2}+{y^2}\overrightarrow e_2^2=4$,
即${x^2}+2xy|{\overrightarrow e_1}|•|{\overrightarrow e_2}|cos{60°}+{y^2}=4$,化简得x2+y2+xy=4.
故答案为:(1)$\sqrt{7}$; (2)x2+y2+xy=4.
点评 正确理解斜坐标系定义和掌握数量积得运算公式是解题的关键.

| A. | $\frac{π}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{3}$或$\frac{2}{3}π$ | D. | $\frac{5}{6}π$或$\frac{π}{6}$ |
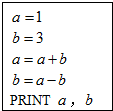
| A. | 1,3 | B. | 4,1 | C. | 4,-2 | D. | 1,-2 |
| A. | 12 | B. | 29 | C. | 55 | D. | 47 |
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{1}{2}$ | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | $-\frac{1}{2}$ |
| A. | $\sqrt{6}$ | B. | $\sqrt{7}$ | C. | $2\sqrt{2}$ | D. | 3 |