题目内容
14.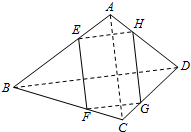 如图所示,ABCD是空间四边形,E、F、G、H分别是四边上的点,并且AC∥面EFGH,BD∥面EFGH,AC=2,BD=4,当EFGH是菱形时,$\frac{AE}{EB}$的值是$\frac{AE}{EB}$.
如图所示,ABCD是空间四边形,E、F、G、H分别是四边上的点,并且AC∥面EFGH,BD∥面EFGH,AC=2,BD=4,当EFGH是菱形时,$\frac{AE}{EB}$的值是$\frac{AE}{EB}$.
分析 由已知条件BEF∽△BAC,从而$\frac{BE}{BA}=\frac{EF}{AC}$,同理,得$\frac{DH}{DA}=\frac{HG}{AC}$,进而推导出△AEH∽△ABD,得$\frac{EH}{BD}$=$\frac{AE}{AB}$,同理得$\frac{EF}{AC}=\frac{BE}{AB}$,由此能求出结果.
解答 解:∵AC∥平面EFGH,AC、EF在平面ABC内,
∴AC∥EF,∴△BEF∽△BAC,
∴$\frac{BE}{BA}=\frac{EF}{AC}$,
同理,得$\frac{DH}{DA}=\frac{HG}{AC}$,
又∵EF=HG,∴$\frac{BE}{BA}=\frac{DH}{DA}$,
∴EH∥BD,∴△AEH∽△ABD,
∴$\frac{EH}{BD}$=$\frac{AE}{AB}$,①,同理得$\frac{EF}{AC}=\frac{BE}{AB}$,②
又∵EH=EF,∴①÷②得:$\frac{AE}{EB}$=$\frac{AC}{BD}$,
∴$\frac{AE}{EB}$=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题考查两条线段的比值的求法,解题时要认真审题,注意三角形相似的性质的合理运用.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案
相关题目
4.设$α∈\{-1,\frac{1}{2},2,3\}$,定义域为R的函数y=xα是奇函数,则α的值为( )
| A. | -1 | B. | 3 | C. | -1,3 | D. | 以上都不对 |
5.用秦九韶算法计算函数f(x)=2x5-3x3+2x2+x-3的值,若x=2,则V3的值是( )
| A. | 12 | B. | 29 | C. | 55 | D. | 47 |
19.sin$\frac{4π}{3}$=( )
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{1}{2}$ | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | $-\frac{1}{2}$ |