题目内容
13.存在正实数b使得关于x的方程$sinx+\sqrt{3}cosx=b$的正根从小到大排成一个等差数列,若点 P(6,b)在直线mx+ny-2=0上(m,n均为正常数),则$\frac{1}{m}+\frac{4}{n}$的最小值为( )| A. | $5+2\sqrt{6}$ | B. | $4\sqrt{3}$ | C. | $8\sqrt{3}$ | D. | $7+4\sqrt{3}$ |
分析 先求出b,再确定3m+n=1,利用“1”的代换,结合基本不等式,即可求出$\frac{1}{m}+\frac{4}{n}$的最小值.
解答 解:由题意,b=2sin(x+$\frac{π}{3}$),
∵存在正实数b使得关于x的方程$sinx+\sqrt{3}cosx=b$的正根从小到大排成一个等差数列,
∴b=2,
∵点 P(6,b)在直线mx+ny-2=0上,
∴6m+2n=2,
∴3m+n=1,
∴$\frac{1}{m}+\frac{4}{n}$=($\frac{1}{m}+\frac{4}{n}$)(3m+n)=3+4+$\frac{n}{m}$+$\frac{12m}{n}$$≥7+2\sqrt{\frac{n}{m}•\frac{12m}{n}}$=7+4$\sqrt{3}$.
故选:D.
点评 本题考查求$\frac{1}{m}+\frac{4}{n}$的最小值,考查基本不等式的运用,确定3m+n=1是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.设F是双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1的左焦点,P是双曲线右支上的动点,A(1,4),则△PAF周长的最小值为$9+\sqrt{41}$.
4.设$α∈\{-1,\frac{1}{2},2,3\}$,定义域为R的函数y=xα是奇函数,则α的值为( )
| A. | -1 | B. | 3 | C. | -1,3 | D. | 以上都不对 |
8.sin65°cos35°-cos65°sin35°=( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | 1 |
18.计算机执行如图的程序段后,输出的结果是( )
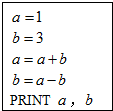
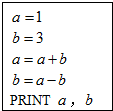
| A. | 1,3 | B. | 4,1 | C. | 4,-2 | D. | 1,-2 |
5.用秦九韶算法计算函数f(x)=2x5-3x3+2x2+x-3的值,若x=2,则V3的值是( )
| A. | 12 | B. | 29 | C. | 55 | D. | 47 |