题目内容
11.与直线4x-3y+5=0关于x轴对称的直线方程为( )| A. | 4x+3y+5=0 | B. | 4x-3y+5=0 | C. | 4x+3y-5=0 | D. | 4x-3y-5=0 |
分析 由条件求得故与直线4x-3y+5=0关于x轴对称的直线的斜率为-$\frac{4}{3}$,且经过点(-$\frac{5}{4}$,0),用点斜式求得要求直线的方程.
解答 解:直线4x-3y+5=0的斜率为$\frac{4}{3}$,与x轴的交点为(-$\frac{5}{4}$,0),
故与直线4x-3y+5=0关于x轴对称的直线的斜率为-$\frac{4}{3}$,且经过点(-$\frac{5}{4}$,0),
故要求的直线方程为y-0=-$\frac{4}{3}$(x+$\frac{5}{4}$),化简可得4x+3y+5=0,
故选:A.
点评 本题主要考查关于x轴对称的两条直线间的关系,用点斜式求直线的方程,属于基础题.

练习册系列答案
相关题目
19.sin$\frac{4π}{3}$=( )
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{1}{2}$ | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | $-\frac{1}{2}$ |
20.向量$\vec a$与向量$\vec a-\vec b$的夹角是$\frac{π}{3}$,$|{\vec a}|=1$,$|{\vec a-\vec b}|=3$,则$|{\vec b}|$等于( )
| A. | $\sqrt{6}$ | B. | $\sqrt{7}$ | C. | $2\sqrt{2}$ | D. | 3 |
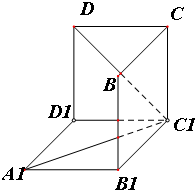 如图是从上下底面处在水平状态下的棱长为a的正方体ABCD-A1B1C1D1中分离出来的.
如图是从上下底面处在水平状态下的棱长为a的正方体ABCD-A1B1C1D1中分离出来的.