题目内容
已知向量
=（
，1），
=（0，-1），
=（k，
），2
-
与
平行，则实数k= ．
| a |
| 3 |
| b |
| c |
| 3 |
| a |
| b |
| c |
考点：平面向量共线（平行）的坐标表示
专题：平面向量及应用
分析：利用已知条件表示出2
-
与
，通过两个向量的平行充要条件，列出方程求解即可．
| a |
| b |
| c |
解答：
解：向量
=（
，1），
=（0，-1），
=（k，
），
∴2
-
=（2
，3）．
∵2
-
与
平行，
∴3k=2
•
．
∴k=2．
故答案为：2．
| a |
| 3 |
| b |
| c |
| 3 |
∴2
| a |
| b |
| 3 |
∵2
| a |
| b |
| c |
∴3k=2
| 3 |
| 3 |
∴k=2．
故答案为：2．
点评：本题考查向量共线的充要条件的应用，向量的坐标运算，基本知识的考查．
练习册系列答案
名师指导期末冲刺卷系列答案
开心蛙口算题卡系列答案
相关题目
代数式x2-9与x2-6x+9的公因式为（ ）
| A、x+3 |
| B、（x+3）2 |
| C、x-3 |
| D、x2+9 |
“x≥0”是“x＞0”的（ ）
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
若A（-1，1）和圆C（x-5）2+（y-7）2=4，一束光线从A点经过X轴反射到圆周C的最短路程是（ ）
| A、-10 | ||
B、6
| ||
C、4
| ||
| D、8 |
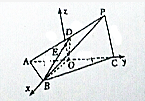如图，在三棱锥P-ABC中，△ABC是正三角形，∠PCA=90°，D是PA的中点，二面角P-AC-B为120°，PC=2，AB=2