题目内容
已知数列{an}满足:a1=1,2n-1an=an-1(n∈N*,n≥2).
(1)求数列{an}的通项公式;
(2)这个数列从第几项开始及以后各项均小于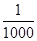 ?
?
(1)求数列{an}的通项公式;
(2)这个数列从第几项开始及以后各项均小于
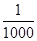 ?
?(1)an=( )
)
(2)第5项
 )
)
(2)第5项
解:(1)n≥2时,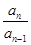 =(
=( )n-1,
)n-1,
故an=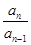 ·…·
·…· ·
· ·a1
·a1
=( )n-1·(
)n-1·( )n-2·…·(
)n-2·…·( )2·(
)2·( )1
)1
=( )1+2+…+(n-1)
)1+2+…+(n-1)
=( )
) ,
,
当n=1时,a1=( )0=1,即n=1时也成立.
)0=1,即n=1时也成立.
∴an=( )
) .
.
(2)∵(n-1)n在[1,+∞)上单调递增,
∴( )
) 在[1,+∞)上单调递减.
在[1,+∞)上单调递减.
当n≥5时, ≥10,an=(
≥10,an=( )
) ≤
≤ .
.
∴从第5项开始及以后各项均小于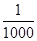 .
.
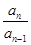 =(
=( )n-1,
)n-1,故an=
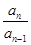 ·…·
·…· ·
· ·a1
·a1=(
 )n-1·(
)n-1·( )n-2·…·(
)n-2·…·( )2·(
)2·( )1
)1=(
 )1+2+…+(n-1)
)1+2+…+(n-1)=(
 )
) ,
,当n=1时,a1=(
 )0=1,即n=1时也成立.
)0=1,即n=1时也成立.∴an=(
 )
) .
.(2)∵(n-1)n在[1,+∞)上单调递增,
∴(
 )
) 在[1,+∞)上单调递减.
在[1,+∞)上单调递减.当n≥5时,
 ≥10,an=(
≥10,an=( )
) ≤
≤ .
.∴从第5项开始及以后各项均小于
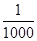 .
.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
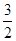 ,前n项和为Sn,且满足2an+1+Sn=3(n∈N*),则满足
,前n项和为Sn,且满足2an+1+Sn=3(n∈N*),则满足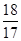 <
<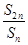 <
<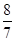 的所有n的和为________.
的所有n的和为________.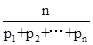 为
为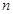 个正数
个正数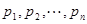 的“均倒数”.若已知数列
的“均倒数”.若已知数列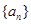 的前
的前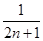 ,又
,又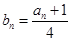 ,则
,则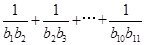 =( )
=( )



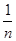 )+f(
)+f(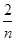 )+f(
)+f(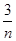 )+…+f(
)+…+f(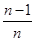 )+f(1).
)+f(1).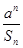 (a∈R)且bn<bn+1对所有正整数n恒成立,求a的取值范围.
(a∈R)且bn<bn+1对所有正整数n恒成立,求a的取值范围.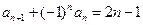 ,则{an}的前
,则{an}的前 项和为
项和为  ,2
,2 ,3
,3 ,4
,4 ,…的前n项和为 .
,…的前n项和为 .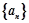 的通项公式为
的通项公式为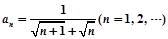 ,
,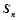 是数列
是数列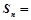 ( )
( )


