题目内容
数列{an}满足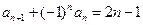 ,则{an}的前
,则{an}的前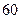 项和为
项和为
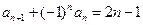 ,则{an}的前
,则{an}的前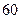 项和为
项和为 1830
法一:由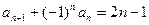 得,
得,
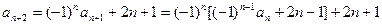
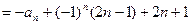 ,
,
即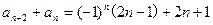 ,也有
,也有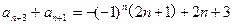 ,两式相加得
,两式相加得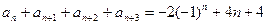 ,设
,设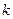 为整数,
为整数,
则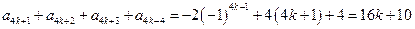 ,
,
于是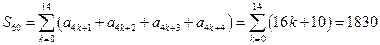
法二:∵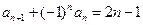
∴a2=a1+1,a3=-a2+3=-(a1+1)+3=-a1+2,a4=a3+5=-a1+7,
a5=a1,a6=a1+9,a7=-a1+2,a8=-a1+15
a9=a1,a10=a1+17,a11=-a1+2,a12=-a1+23
a13=a1,a14=a1+25,a15=-a1+2,a16=-a1+31
∴a1+a2+a3+a4=1+2+7=10,
a5+a6+a7+a8=9+2+15=26,
a9+a10+a11+a12=17+2+23=42,
a13+a14+a15+a16=25+2+31=58,
由此发现,此数列的每四项之和为一常数,且每四项和构成一首项为10,公差为16的等差数列,而60=15×4,所以{an}的前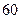 项和为15×10+
项和为15×10+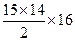 =1830
=1830
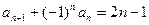 得,
得,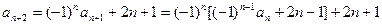
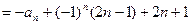 ,
,即
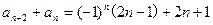 ,也有
,也有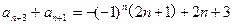 ,两式相加得
,两式相加得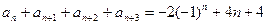 ,设
,设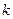 为整数,
为整数,则
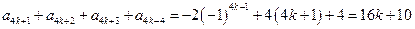 ,
,于是
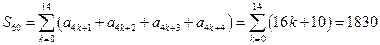
法二:∵
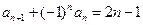
∴a2=a1+1,a3=-a2+3=-(a1+1)+3=-a1+2,a4=a3+5=-a1+7,
a5=a1,a6=a1+9,a7=-a1+2,a8=-a1+15
a9=a1,a10=a1+17,a11=-a1+2,a12=-a1+23
a13=a1,a14=a1+25,a15=-a1+2,a16=-a1+31
∴a1+a2+a3+a4=1+2+7=10,
a5+a6+a7+a8=9+2+15=26,
a9+a10+a11+a12=17+2+23=42,
a13+a14+a15+a16=25+2+31=58,
由此发现,此数列的每四项之和为一常数,且每四项和构成一首项为10,公差为16的等差数列,而60=15×4,所以{an}的前
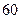 项和为15×10+
项和为15×10+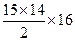 =1830
=1830
练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
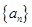 是公差不为零的等差数列,
是公差不为零的等差数列,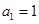 ,且
,且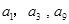 成等比数列.
成等比数列.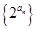 的前
的前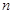 项和
项和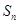 .
.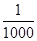 ?
?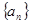 中,
中,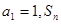 是数列
是数列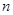 项和,对任意
项和,对任意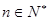 ,有
,有 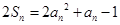 .
.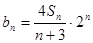 ,求数列
,求数列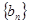 的前
的前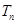 .
.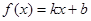 的图像经过点
的图像经过点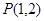 和
和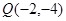 ,令
,令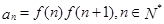 ,记数列
,记数列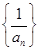 的前项和为
的前项和为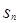 ,当
,当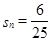 时,
时,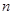 的值等于( )
的值等于( )



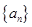 是等差数列,且a2=3,并且d=2,则
是等差数列,且a2=3,并且d=2,则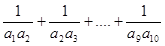 =_______
=_______ 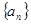 ,规定
,规定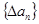 为数列
为数列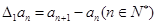 .对于正整数
.对于正整数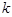 ,规定
,规定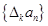 为
为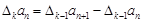 .若数列
.若数列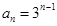 ,则
,则 .
.