题目内容
设数列{an}的首项a1=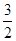 ,前n项和为Sn,且满足2an+1+Sn=3(n∈N*),则满足
,前n项和为Sn,且满足2an+1+Sn=3(n∈N*),则满足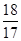 <
<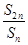 <
<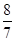 的所有n的和为________.
的所有n的和为________.
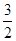 ,前n项和为Sn,且满足2an+1+Sn=3(n∈N*),则满足
,前n项和为Sn,且满足2an+1+Sn=3(n∈N*),则满足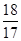 <
<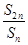 <
<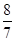 的所有n的和为________.
的所有n的和为________.7
由2an+1+Sn=3得2an+Sn-1=3(n≥2),两式相减,得2an+1-2an+an=0,化简得2an+1=an(n≥2),即 =
= (n≥2),由已知求出a2=
(n≥2),由已知求出a2= ,易得
,易得 =
= ,所以数列{an}是首项为a1=
,所以数列{an}是首项为a1=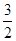 ,公比为q=
,公比为q= 的等比数列,所以Sn=
的等比数列,所以Sn= =3[1-(
=3[1-( )n],S2n=3[1-(
)n],S2n=3[1-( )2n]代入
)2n]代入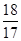 <
<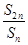 <
<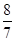 ,可得
,可得 <(
<( )n<
)n< ,解得n=3或4,所以所有n的和为7.
,解得n=3或4,所以所有n的和为7.
 =
= (n≥2),由已知求出a2=
(n≥2),由已知求出a2= ,易得
,易得 =
= ,所以数列{an}是首项为a1=
,所以数列{an}是首项为a1=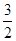 ,公比为q=
,公比为q= 的等比数列,所以Sn=
的等比数列,所以Sn= =3[1-(
=3[1-( )n],S2n=3[1-(
)n],S2n=3[1-( )2n]代入
)2n]代入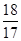 <
<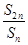 <
<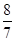 ,可得
,可得 <(
<( )n<
)n< ,解得n=3或4,所以所有n的和为7.
,解得n=3或4,所以所有n的和为7.
练习册系列答案
相关题目
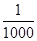 ?
? 的前
的前 项和
项和 ,数列
,数列 满足
满足 .
. 的前
的前 .
. 的前n项和为
的前n项和为 ,且
,且 ,则
,则 =
= +
+ + +
+ + ,则M的值为( )
,则M的值为( )



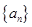 是等差数列,且a2=3,并且d=2,则
是等差数列,且a2=3,并且d=2,则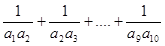 =_______
=_______