题目内容
5.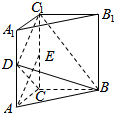 如图,三棱柱ABC-A1B1C1中,侧棱垂直于底面,∠ACB=90°,AC=$\frac{1}{2}$AA1,D、E分别是棱AA1、CC1的中点.
如图,三棱柱ABC-A1B1C1中,侧棱垂直于底面,∠ACB=90°,AC=$\frac{1}{2}$AA1,D、E分别是棱AA1、CC1的中点.(1)证明:AE∥平面BDC1;
(2)证明:DC1⊥平面BDC.
分析 (1)欲证明AE∥平面BDC1,只需推知AE∥DC1即可;
(2)欲证明DC1⊥平面BDC,只需证得DC1与平面BDC内的两条相交线垂直即可.
解答  证明:(1)因为D、E分别是棱AA1、CC1的中点,AC=$\frac{1}{2}$AA1,
证明:(1)因为D、E分别是棱AA1、CC1的中点,AC=$\frac{1}{2}$AA1,
所以AD∥C1E,且AD=C1E,
所以四边形DAEC1是平行四边形,
所以AE∥DC1.
因为DC1?平面BDC1,
所以AE∥平面BDC1;
(2)由题意知,BC⊥CC1,BC⊥AC.
所以BC⊥面ACC1A1.
又DC1?面ACC1A1,
所以DC1⊥BC.
在矩形ACC1A1中,因为AC=$\frac{1}{2}$AA1,D是棱AA1的中点,
所以DC1⊥DC.
因为DC1⊥BC,DC1⊥DC,且BC∩DC=C,
所以DC1⊥平面BDC.
点评 本题考查了线面平行、线面垂直的判定定理,是一道中档题.解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.已知扇形的圆心角为$\frac{3}{4}π$,半径为4,则扇形的面积S为( )
| A. | 3π | B. | 4π | C. | 6π | D. | 2π |
17.从1,2,3,4,5这5个数中取出2个数,使得剩下的3个数的平均数与原来5个数的平均数不变,则不同的取法共有( )
| A. | 1种 | B. | 2种 | C. | 3种 | D. | 4种 |
14.测谎仪是一种通过人的脑电波的变化,来判断被测人是否说谎的一种仪器,对于某一语言刺激,没说谎的人的脑电波一般是正弦波,而说谎的人的脑电波则是锯齿波,下面是询问某一问题时,一个没说谎的人脑电波的数据:
若就同一个问题询问另一个人时,得到以下脑电波数据:当t=0.1时,y=-1,当t=0.5时,y=3.6,根据这些数据,判断此人是否说谎?
| t | 0 | 0.2 | 0.4 | 0.6 | 0.8 |
| y | -4 | 0 | 4 | 0 | -4 |
15.cos225°的值等于( )
| A. | $-\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | -1 | D. | 1 |