题目内容
【题目】对于定义在区间![]() 上的函数
上的函数![]() ,若任给
,若任给![]() ,均有
,均有![]() ,则称函数
,则称函数![]() 在区间
在区间![]() 上是封闭.
上是封闭.
(1)试判断![]() 在区间
在区间![]() 上是否封闭,并说明理由;
上是否封闭,并说明理由;
(2)若函数![]() 在区间
在区间![]() 上封闭,求
上封闭,求![]() 的取值范围.
的取值范围.
【答案】(1)不封闭,理由见解析;(2)![]() .
.
【解析】
(1)求出二次函数![]() 在区间
在区间![]() 上的值域,结合题中定义判断即可;
上的值域,结合题中定义判断即可;
(2)将函数![]() 的解析式变形为
的解析式变形为![]() ,分类讨论
,分类讨论![]() 的取值,求得函数
的取值,求得函数![]() 在区间
在区间![]() 上的值域,转化为函数
上的值域,转化为函数![]() 区间
区间![]() 上的值域为
上的值域为![]() 的子集,由此可求得实数
的子集,由此可求得实数![]() 的取值范围.
的取值范围.
(1)![]() ,
,
当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增,
上单调递增,
所以,![]() ,
,![]() ,
,
所以,函数![]() 在区间
在区间![]() 上的值域为
上的值域为![]() ,
,
![]() ,因此,函数
,因此,函数![]() 在区间
在区间![]() 上不封闭;
上不封闭;
(2)![]() .
.
①当![]() 时,对任意的
时,对任意的![]() ,
,![]() ,
,
此时,函数![]() 在区间
在区间![]() 上封闭;
上封闭;
②当![]() 时,
时,![]() ,此时函数
,此时函数![]() 在区间
在区间![]() 上单调递增,
上单调递增,
则当![]() 时,
时,![]() ,则
,则![]() ,
,
所以,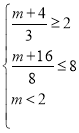 ,解得
,解得![]() ;
;
③当![]() 时,
时,![]() ,此时函数
,此时函数![]() 在区间
在区间![]() 上单调递减,
上单调递减,
则当![]() 时,
时,![]() ,则
,则![]() ,
,
所以,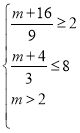 ,解得
,解得![]() .
.
综上所述,实数![]() 的取值范围是
的取值范围是![]() .
.

练习册系列答案
相关题目
【题目】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费![]() (单位:万元)对年销售量
(单位:万元)对年销售量![]() (单位:吨)和年利润
(单位:吨)和年利润![]() (单位:万元)的影响.对近六年的年宣传费
(单位:万元)的影响.对近六年的年宣传费![]() 和年销售量
和年销售量![]() (
(![]() )的数据作了初步统计,得到如下数据:
)的数据作了初步统计,得到如下数据:
年份 |
|
|
|
|
|
|
年宣传费 |
|
|
|
|
|
|
年销售量 |
|
|
|
|
|
|
经电脑模拟,发现年宣传费![]() (万元)与年销售量
(万元)与年销售量![]() (吨)之间近似满足关系式
(吨)之间近似满足关系式![]() (
(![]() ).对上述数据作了初步处理,得到相关的值如表:
).对上述数据作了初步处理,得到相关的值如表:
|
|
|
|
|
|
|
|
(1)根据所给数据,求![]() 关于
关于![]() 的回归方程;
的回归方程;
(2)已知这种产品的年利润![]() 与
与![]() ,
,![]() 的关系为
的关系为![]() 若想在
若想在![]() 年达到年利润最大,请预测
年达到年利润最大,请预测![]() 年的宣传费用是多少万元?
年的宣传费用是多少万元?
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 中的斜率和截距的最小二乘估计分别为
中的斜率和截距的最小二乘估计分别为 ,
,![]()
