[题目]如图.在三棱锥P-ABC中.PA⊥平面ABC.AC⊥BC.D为PC中点.E为AD中点.PA＝AC＝2.BC＝1．(1)求证:AD⊥平面PBC:(2)求PE与平面ABD所成角的正弦值．题目和参考答案——青夏教育精英家教网—

题目内容

【题目】如图，在三棱锥P—ABC中，PA⊥平面ABC，AC⊥BC，D为PC中点，E为AD中点，PA＝AC＝2，BC＝1．

（1）求证：AD⊥平面PBC：

（2）求PE与平面ABD所成角的正弦值．

【答案】（1）证明见解析；（2）.

【解析】

（1）先通过线面垂直的判定定理，得出平面PAC，所以，由等腰三角形的性质可得，，可得最后结果.

（2）以C为坐标原点建立空间直角坐标系，求A，B，P，D，E点的坐标，求平面ABD的法向量为，利用线面角的公式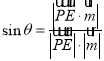即可得出结果.

（1）证明：∵平面ABC，∴

又因为，

∴平面PAC，∴．

∵，D为PC中点，

∴，又∵，

∴平面PBC；

（2）以C为坐标原点建立如图空间直角坐标系

，，，∴，，

∴，，．

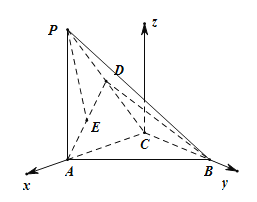
设平面ABD的法向量为，

则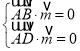，令，则，得．

设PE与平面ABD所成角为，则

．

练习册系列答案

相关题目

【题目】在平面直角坐标系中，已知曲线与曲线，（为参数）．以坐标原点为极点，轴的正半轴为极轴建立极坐标系．

（1）写出曲线，的极坐标方程；

（2）在极坐标系中，已知与，的公共点分别为，，，当时，求的值．

【题目】在直角坐标系中，曲线的参数方程为（为参数），以坐标原点为极点，以轴正半轴为极轴，建立极坐标系，直线的极坐标方程为.

（1）求的普通方程和的直角坐标方程；

（2）直线与轴的交点为，经过点的直线与曲线交于两点，若，求直线的倾斜角.

【题目】已知函数，mR.

（1）若m＝﹣1，求函数在区间[,e]上的最小值；

（2）若m＞0，求函数的单调增区间.

【题目】如图，在平面直角坐标系xOy中，椭圆的左焦点为，右顶点为，上顶点为．

（1）已知椭圆的离心率为，线段中点的横坐标为，求椭圆的标准方程；

（2）已知△外接圆的圆心在直线上，求椭圆的离心率的值．

【题目】对于定义在区间上的函数，若任给，均有，则称函数在区间上是封闭.

（1）试判断在区间上是否封闭，并说明理由；

（2）若函数在区间上封闭，求的取值范围.

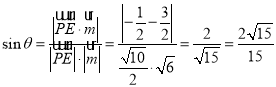【题目】癌症是迄今为止人类尚未攻克的疾病之一，目前，癌症只能尽量预防．某医学中心推出了一种抗癌症的制剂，现对20位癌症病人，进行医学试验测试药效，测试结果分为“病人死亡”和“病人存活”，现对测试结果和药物剂量（单位：）进行统计，规定病人在服用（包括）以上为“足量”，否则为“不足量”，统计结果显示，这20病人