题目内容
18.已知中心在坐标原点的椭圆与双曲线有公共焦点,且左、右焦点分别为F1、F2,这两条曲线在第一象限的交点为P,△PF1F2是以PF1为底边的等腰三角形,若|PF1|=10,设椭圆与双曲线的离心率分别为e1,e2,则e1+e2的取值范围是( )| A. | ($\frac{5}{4}$,+∞) | B. | ($\frac{4}{3}$,+∞) | C. | ($\frac{3}{2}$,+∞) | D. | ($\frac{5}{3}$,+∞) |
分析 设椭圆和双曲线的半焦距为c,|PF1|=m,|PF2|=n,(m>n),由条件可得m=10,n=2c,再由椭圆和双曲线的定义可得a1=5+c,a2=5-c,(c<5),运用三角形的三边关系求得c的范围,再由离心率公式,计算即可得到所求范围.
解答 解:设椭圆和双曲线的半焦距为c,|PF1|=m,|PF2|=n,(m>n),
由于△PF1F2是以PF1为底边的等腰三角形.若|PF1|=10,
即有m=10,n=2c,
由椭圆的定义可得m+n=2a1,
由双曲线的定义可得m-n=2a2,
即有a1=5+c,a2=5-c,(c<5),
再由三角形的两边之和大于第三边,可得2c+2c>10,
可得c>$\frac{5}{2}$,即有$\frac{5}{2}$<c<5.
由离心率公式可得e1+e2=$\frac{c}{{a}_{1}}$+$\frac{c}{{a}_{2}}$=$\frac{c}{5+c}$+$\frac{c}{5-c}$=$\frac{10c}{25-{c}^{2}}$=$\frac{10}{\frac{25}{c}-c}$,
∵f(x)=$\frac{25}{x}-x$在($\frac{5}{2}$,5)上是减函数,
∴0=$\frac{25}{5}-5$<$\frac{25}{c}-c$<$\frac{25}{\frac{5}{2}}-\frac{5}{2}$=$\frac{15}{2}$,
∴$\frac{4}{3}$=$\frac{10}{\frac{15}{2}}$<$\frac{10}{\frac{25}{c}-c}$<+∞,
故选:B.
点评 本题考查椭圆和双曲线的定义和性质,考查离心率的求法,考查三角形的三边关系,考查运算能力,属于中档题.

练习册系列答案
相关题目
10.在△ABC内部随机取一点P,则事件“△PBC”的面积不大于△ABC面积的$\frac{1}{4}$”的概率是( )
| A. | $\frac{7}{16}$ | B. | $\frac{9}{16}$ | C. | $\frac{5}{9}$ | D. | $\frac{4}{9}$ |
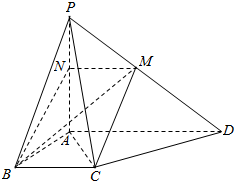 如图所示,四棱锥P-ABCD的底面ABCD是直角梯形,BC∥AD,AB⊥AD,AB=BC=$\frac{1}{2}$AD,PA⊥底面ABCD,过BC的平面交PD于M,交PA与N(M与D不重合).
如图所示,四棱锥P-ABCD的底面ABCD是直角梯形,BC∥AD,AB⊥AD,AB=BC=$\frac{1}{2}$AD,PA⊥底面ABCD,过BC的平面交PD于M,交PA与N(M与D不重合).
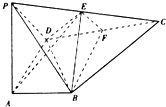 如图,在四棱锥P-ABCD中,AB∥CD,PA⊥AD,CD⊥AD,PA=AD=CD=2AB,E,F分别为PC,CD的中点,DE=EC.
如图,在四棱锥P-ABCD中,AB∥CD,PA⊥AD,CD⊥AD,PA=AD=CD=2AB,E,F分别为PC,CD的中点,DE=EC.