题目内容
1.已知a∈R,f(x)=x|x-a|.(1)判断f(x)的奇偶性并证明;
(2)当a>0时,求f(x)在[0,1]的最大值.
分析 (1)讨论a=0时与a≠0时的奇偶性,然后定义定义进行证明即可;
(2)当a>0时,求出函数f(x)=x|x-a|的表达式,即可求出在区间[0,1]上的最大值.
解答 解:(1)由题意可知函数f(x)的定义域为R.
当a=0时f(x)=x|x-a|=x|x|,为奇函数.
当a≠0时,f(x)=x|x-a|,
f(1)=|1-a|,f(-1)=-|1+a|,
f(-x)≠f(x)且f(-x)≠-f(x),
∴此时函数f(x)为非奇非偶函数.
(2)由题意可得f(x)=$\left\{\begin{array}{l}{{x}^{2}-ax=(x-\frac{a}{2})^{2}-\frac{{a}^{2}}{4},x≥a}\\{ax-{x}^{2}=-(x-\frac{a}{2})^{2}+\frac{{a}^{2}}{4},x<a}\end{array}\right.$,
由于a>0且0≤x≤1,结合函数f(x)的图象可知,
由${x}^{2}-ax=\frac{{a}^{2}}{4},即x=(\frac{1+\sqrt{2}}{2})a$,
当$\frac{a}{2}≥1$,即a≥2时,f(x)在[0,1]上单调递增,
∴f(x)的最大值为f(1)=a-1;
当$\frac{1}{2}<1<(\frac{1+\sqrt{2}}{2})a$,
即$2(\sqrt{2}-1)≤a<2$时,f(x)在[0,$\frac{a}{2}$]上递增,在[$\frac{a}{2}$,a]上递减,
∴f(x)的最大值为f($\frac{a}{2}$)=$\frac{{a}^{2}}{4}$;
当$(\frac{1+\sqrt{2}}{2})a<1$,即$0<a<2(\sqrt{2}-1)$时,
f(x)在[0,$\frac{a}{2}$]上递增,在[$\frac{a}{2}$,a]上递减,在[a,1]上递增,
∴f(x)的最大值为f(1)=1-a.
点评 本题主要考查函数奇偶性的判断,以及分段函数的最值的求法,考查学生的运算能力.

| A. | $\frac{7}{16}$ | B. | $\frac{9}{16}$ | C. | $\frac{5}{9}$ | D. | $\frac{4}{9}$ |
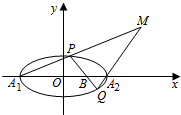 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右准线l的方程为x=$\frac{4\sqrt{3}}{3}$,焦距为2$\sqrt{3}$.
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右准线l的方程为x=$\frac{4\sqrt{3}}{3}$,焦距为2$\sqrt{3}$.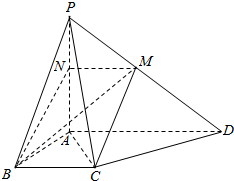 如图所示,四棱锥P-ABCD的底面ABCD是直角梯形,BC∥AD,AB⊥AD,AB=BC=$\frac{1}{2}$AD,PA⊥底面ABCD,过BC的平面交PD于M,交PA与N(M与D不重合).
如图所示,四棱锥P-ABCD的底面ABCD是直角梯形,BC∥AD,AB⊥AD,AB=BC=$\frac{1}{2}$AD,PA⊥底面ABCD,过BC的平面交PD于M,交PA与N(M与D不重合).