题目内容
(本小题满分12分)
设数列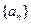 的前
的前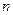 项和为
项和为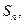 已知
已知

(I)设 ,证明数列
,证明数列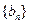 是等比数列
是等比数列 

(II)求数列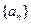 的通项公式.
的通项公式.
设数列
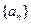 的前
的前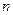 项和为
项和为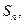 已知
已知

(I)设
 ,证明数列
,证明数列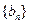 是等比数列
是等比数列 

(II)求数列
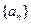 的通项公式.
的通项公式.:(I)由 成立,则有
成立,则有 两式相减得
两式相减得 ,变形为
,变形为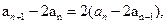 即
即 ,由
,由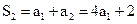 得
得
于是 ,所以数列
,所以数列 是首项为3公比是2的等比数列.
是首项为3公比是2的等比数列.
(II)解法一:由⑴得 即
即 所以
所以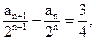 且
且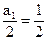 ,
,
于是数列 是首项为
是首项为 ,公差为
,公差为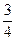 的等差数列,所以
的等差数列,所以 ,
,
即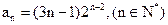 .
.
解法二:由⑴得 即
即

 ,
,


 成立,则有
成立,则有 两式相减得
两式相减得 ,变形为
,变形为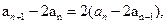 即
即 ,由
,由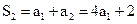 得
得
于是
 ,所以数列
,所以数列 是首项为3公比是2的等比数列.
是首项为3公比是2的等比数列.(II)解法一:由⑴得
 即
即 所以
所以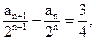 且
且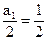 ,
,于是数列
 是首项为
是首项为 ,公差为
,公差为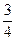 的等差数列,所以
的等差数列,所以 ,
,即
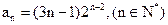 .
.解法二:由⑴得
 即
即

 ,
,

:由递推式进行递推,可以寻找规律,根据(I)要求(即提示)变形即可.证明数列最常用的方法是定义法,想到这一点,第(I)题就解决了.根据两个小题的联系,进一步变形寻找规律,求出通项.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 中,
中,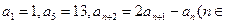 N*),数列
N*),数列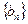 中,
中,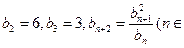 N*),已知点
N*),已知点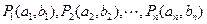
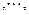 则向量
则向量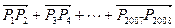 的坐标为( )
的坐标为( )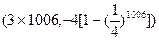
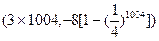
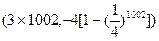
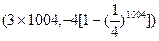
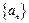 的前
的前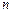 项和为
项和为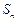 ,且
,且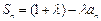 ,其中
,其中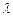 为常数,且
为常数,且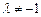 、0.(1)证明:数列
、0.(1)证明:数列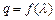 ,数列
,数列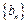 满足
满足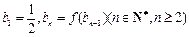 ,求数列
,求数列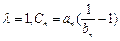 ,数列
,数列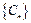 的前
的前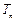 ,求证:当
,求证:当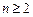 时,
时,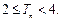
 的前
的前 项和为
项和为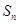 ,若
,若 ,则
,则 的最大值为____。
的最大值为____。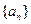 中,已知
中,已知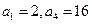


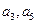 分别为等差数列
分别为等差数列 的第3项和第5项,试求数列
的第3项和第5项,试求数列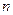 项和
项和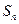 。
。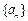 的通项公式
的通项公式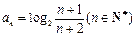 ,设
,设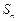 ,则使
,则使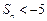 成立的自然数n( )
成立的自然数n( )
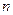 项正项数列为
项正项数列为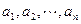 ,
, 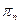 为其前
为其前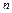 项的积,定义
项的积,定义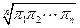 为“叠乘积”.如果有2005项的正项数列
为“叠乘积”.如果有2005项的正项数列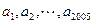 的“叠乘积”为
的“叠乘积”为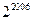 ,则有2006项的数列
,则有2006项的数列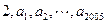 的“叠乘积”为 ( )
的“叠乘积”为 ( )