题目内容
一个项数为偶数的等差数列,奇数项的和与偶数项的和分别为24和30.若最后一项比第一项多10.5,则该数列的项数为( )
| A.18 | B.12 | C.10 | D.8 |
假设数列有2n项,公差为d,
因为奇数项之和与偶数项之和分别是24与30
所以S偶-S奇=30-24=nd,
即nd=6①.
又a2n-a1=10.5
即a1+(2n-1)d-a1=10.5
所以(2n-1)d=10.5②.
联立①②得:n=4.
则这个数列一共有2n项,即8项.
故选D.
因为奇数项之和与偶数项之和分别是24与30
所以S偶-S奇=30-24=nd,
即nd=6①.
又a2n-a1=10.5
即a1+(2n-1)d-a1=10.5
所以(2n-1)d=10.5②.
联立①②得:n=4.
则这个数列一共有2n项,即8项.
故选D.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
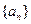 中,
中, 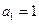 ,
, 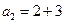 ,
, 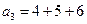 ,
, 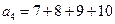 ,…,
,…,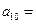 ( )
( )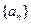 的前
的前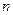 项和为
项和为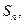 已知
已知

 ,证明数列
,证明数列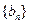 是等比数列
是等比数列 

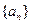 中,
中,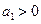 ,且满足
,且满足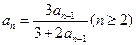 ,则数列
,则数列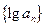 是:( )
是:( )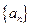 为等差数列,
为等差数列,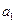 +
+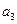 +
+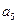 =105,
=105,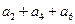 =99,以
=99,以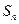 表示
表示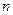 项和,则使得
项和,则使得