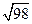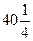题目内容
求圆心在直线x+y=0上，且过两圆x2+y2-2x+10y-24=0，x2+y2+2x+2y-8=0的交点的圆的方程.
圆的方程为(x+3)2+(y-3)2=10.
解方程组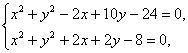
得交点坐标分别为(0,2),(-4,0).
设所求圆的圆心坐标为(a,-a),
则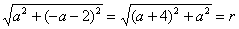
.
解得a=-3,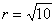
.
因此,圆的方程为(x+3)2+(y-3)2=10.
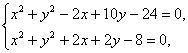得交点坐标分别为(0,2),(-4,0).设所求圆的圆心坐标为(a,-a),
则
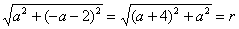.解得a=-3,
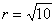.因此,圆的方程为(x+3)2+(y-3)2=10.
练习册系列答案
相关题目
中,若两点
、
，
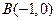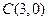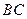边中线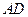
的长度为4,则点A的轨迹方程为( )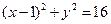
)
)
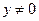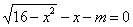有实数解,则实数m的取值范围为( )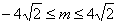 
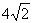
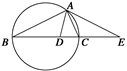
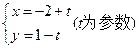被圆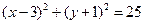
所截得的弦长为（ ）
