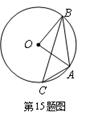
题目内容
过点A(-1,4),并且与圆(x-3)2+(y+1)2=5相切于点B(2,1)的圆的方程是___________.
(x-1)2+(y-3)2=5
设圆心为(a,b),
∵三点(3,-1)、(2,1)与(a,b)共线,
∴2a+b-5="0. " ①
又两点A(-1,4)与B(2,1)都在圆上,
∴(a+1)2+(b-4)2=(a-2)2+(b-1)2,
即a-b+2="0. " ②
由①②联立解得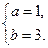
半径r=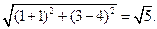
∴所求圆的方程为(x-1)2+(y-3)2=5.
∵三点(3,-1)、(2,1)与(a,b)共线,
∴2a+b-5="0. " ①
又两点A(-1,4)与B(2,1)都在圆上,
∴(a+1)2+(b-4)2=(a-2)2+(b-1)2,
即a-b+2="0. " ②
由①②联立解得
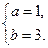
半径r=
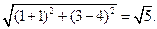
∴所求圆的方程为(x-1)2+(y-3)2=5.

练习册系列答案
相关题目
 ,
,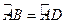 ,过A点的切线交CB的延长线于E点.
,过A点的切线交CB的延长线于E点.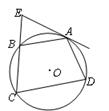
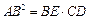 .
.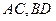 为圆
为圆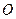 :
: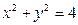 的两条互相垂直的弦,垂足为
的两条互相垂直的弦,垂足为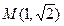
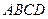 的面积的最大值,并且取得最大值时
的面积的最大值,并且取得最大值时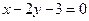

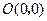 ,
,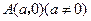 距离的比为
距离的比为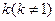 的点的轨迹,求此曲线的方程,并判断曲线的形状.
的点的轨迹,求此曲线的方程,并判断曲线的形状. 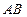 是圆
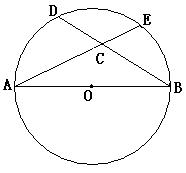
是圆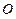 的直径,
的直径,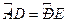 ,
,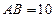 ,
,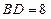 ,则
,则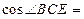 .
.
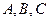 是圆
是圆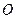 上的点,且
上的点,且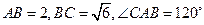 ,则
,则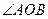 对应的劣弧长为 .
对应的劣弧长为 .