题目内容
【题目】已知函数![]() ,
,![]() .
.
(1)当![]() 时,求曲线
时,求曲线![]() 与
与![]() 的公切线方程:
的公切线方程:
(2)若![]() 有两个极值点
有两个极值点![]() ,
,![]() ,且
,且![]() ,求实数a的取值范围.
,求实数a的取值范围.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)利用求导,分别求出两条曲线的切线方程.由题知两条切线重合,则可列出方程组,解得两个切点的横坐标,从而求出切线方程;
(2)求![]() 的导函数,其零点即为极值点
的导函数,其零点即为极值点![]() ,
,![]() ,则
,则![]() .根据
.根据![]() ,可设
,可设![]() ,解得
,解得![]() ,由此构造函数
,由此构造函数![]() ,利用导函数求出
,利用导函数求出![]() 的值域
的值域![]() ,也即是
,也即是![]() 的范围.由
的范围.由![]() 构造函数
构造函数![]() ,求出其值域,也即是实数
,求出其值域,也即是实数![]() 的取值范围.
的取值范围.
解:(1)![]() 时,
时,![]() ,
,
设曲线![]() 上的切点为
上的切点为![]() ,则切线方程为
,则切线方程为![]() ,
,
设曲线![]() 上的切点为
上的切点为![]() ,则切线方程为
,则切线方程为![]()
由两条切线重合得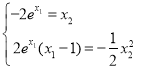 ,则
,则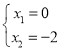 ,
,
所以,公切线方程为![]() ;
;
(2)![]() ,
,
![]() ,设其零点为
,设其零点为![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
令![]() ,可得
,可得![]() ,则
,则![]()
令![]() ,
,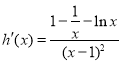 ,
,
又令![]() ,
,![]() ,则
,则![]() 单调递减,
单调递减,
![]() ,
,![]() ,
,![]() 单调递减,
单调递减,
![]() ,易知
,易知![]() ,
,![]() ,
,
令![]() ,
,![]() ,
,
则![]() 在
在![]() 上递增,
上递增,
![]()

 优学名师名题系列答案
优学名师名题系列答案【题目】近年来,国家相关政策大力鼓励创新创业种植业户小李便是受益者之一,自从2017年毕业以来,其通过自主创业而种植的某种农产品广受市场青睐,他的种植基地也相应地新增加了一个平时小李便带着部分员工往返于新旧基地之间进行科学管理和经验交流,新旧基地之间开车单程所需时间为![]() ,由于不同时间段车流量的影响,现对50名员工往返新旧基地之间的用时情况进行统计,结果如下:
,由于不同时间段车流量的影响,现对50名员工往返新旧基地之间的用时情况进行统计,结果如下:
| 30 | 35 | 40 | 45 | 50 |
频数(人) | 10 | 20 | 10 | 5 | 5 |
(1)若有50名员工参与调查,现从单程时间在35分钟,40分钟,45分钟的人员中按分层抽样的方法抽取7人,再从这7人中随机抽取3人进行座谈,用![]() 表示抽取的3人中时间在40分钟的人数,求
表示抽取的3人中时间在40分钟的人数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(2)某天,小李需要从旧基地驾车赶往新基地召开一个20分钟的紧急会议,结束后立即返回旧基地.(以50名员工往返新旧基地之间的用时的频率作为用时发生的概率)
①求小李从离开旧基地到返回旧基地共用时间不超过110分钟的概率;
②若用随机抽样的方法从旧基地抽取8名骨干员工陪同小李前往新基地参加此次会议,其中有![]() 名员工从离开旧基地到返回旧基地共用时间不超过110分钟,求随机变量
名员工从离开旧基地到返回旧基地共用时间不超过110分钟,求随机变量![]() 的方差.
的方差.
【题目】为响应“文化强国建设”号召,并增加学生们对古典文学的学习兴趣,雅礼中学计划建设一个古典文学熏陶室.为了解学生阅读需求,随机抽取200名学生做统计调查.统计显示,男生喜欢阅读古典文学的有64人,不喜欢的有56人;女生喜欢阅读古典文学的有36人,不喜欢的有44人.
(1)能否在犯错误的概率不超过0.25的前提下认为喜欢阅读古典文学与性别有关系?
(2)为引导学生积极参与阅读古典文学书籍,语文教研组计划牵头举办雅礼教育集团古典文学阅读交流会.经过综合考虑与对比,语文教研组已经从这200人中筛选出了5名男生代表和4名女生代表,其中有3名男生代表和2名女生代表喜欢古典文学.现从这9名代表中任选3名男生代表和2名女生代表参加交流会,记![]() 为参加交流会的5人中喜欢古典文学的人数,求
为参加交流会的5人中喜欢古典文学的人数,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
附: ,其中
,其中![]() .
.
参考数据:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 |