题目内容
【题目】已知椭圆![]() :
:![]() 的左、右顶点分别为C、D,且过点
的左、右顶点分别为C、D,且过点![]() ,P是椭圆上异于C、D的任意一点,直线PC,PD的斜率之积为
,P是椭圆上异于C、D的任意一点,直线PC,PD的斜率之积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)O为坐标原点,设直线CP交定直线x = m于点M,当m为何值时,![]() 为定值.
为定值.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)设![]() ,根据题意可求得
,根据题意可求得![]() ,再代
,再代![]() 入椭圆方程即可求解.
入椭圆方程即可求解.
(2)根据(1)中的结论, 设直线![]() ,并联立与椭圆的方程,求得
,并联立与椭圆的方程,求得![]() ,
,![]() ,再表达出
,再表达出![]() ,根据恒成立问题求得系数的关系即可.也可直接设
,根据恒成立问题求得系数的关系即可.也可直接设![]() 表达出
表达出![]() ,利用
,利用![]() 满足椭圆的方程进行化简,同理可得m的值.
满足椭圆的方程进行化简,同理可得m的值.
解:(1)椭圆![]() 过点
过点![]() ,∴
,∴![]() ,①
,①
又因为直线![]() 的斜率之积为
的斜率之积为![]() ,故
,故![]() .
.
又![]() .即
.即![]() ,②
,②
联立①②得![]() .
.
∴所求的椭圆方程为![]() .
.
(2)方法1:由(1)知,![]() .由题意可设
.由题意可设![]() ,
,
令x=m,得![]() .又设
.又设![]()
由 整理得:
整理得:![]() .
.
∵![]() ,∴
,∴![]() ,
,![]() ,
,
所以![]() ,
,
∴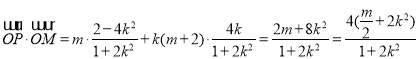 ,
,
要使![]() 与k无关,只需
与k无关,只需![]() ,此时
,此时![]() 恒等于4.
恒等于4.
∴![]()
方法2::设![]() ,则
,则![]() ,令x=m,得
,令x=m,得![]() ,
,
∴![]()
由![]() 有
有![]() ,
,
所以![]() ,
,
要使![]() 与
与![]() 无关,只须
无关,只须![]() ,此时
,此时![]() .
.
∴![]()

练习册系列答案
相关题目