题目内容
【题目】已知函数![]() 有两个零点
有两个零点![]() 、
、![]() .
.
(1)求实数![]() 的取值范围;
的取值范围;
(2)若![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)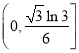 .
.
【解析】
(1)由![]() 得
得![]() ,构造函数
,构造函数![]() ,利用导数分析函数
,利用导数分析函数![]() 的单调性与极值,作出函数
的单调性与极值,作出函数![]() 的图象,数形结合可得出实数
的图象,数形结合可得出实数![]() 的取值范围;
的取值范围;
(2)由题意推导出![]() ,分
,分![]() 和
和![]() 两种情况讨论,结合
两种情况讨论,结合![]() 以及函数
以及函数![]() 的单调性得出
的单调性得出![]() 的取值范围,再由
的取值范围,再由![]() 以及函数
以及函数![]() 的单调性可求得实数
的单调性可求得实数![]() 的取值范围.
的取值范围.
(1)![]() ,令
,令![]() ,可得
,可得![]() ,
,
构造函数![]() ,则直线
,则直线![]() 与函数
与函数![]() 的图象有两个交点.
的图象有两个交点.
![]() ,令
,令![]() ,得
,得![]() ,列表如下:
,列表如下:
|
|
|
|
|
|
|
|
|
| 极大值 |
|
所以,函数![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ,且在
,且在![]() 处取得极大值
处取得极大值![]() .
.
当![]() 时,
时,![]() ;当
;当![]() 时,
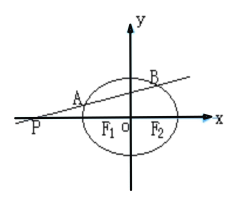
时,![]() ,如下图所示:
,如下图所示:

如上图可知,当![]() 时,直线
时,直线![]() 与函数
与函数![]() 的图象有两个交点,
的图象有两个交点,
因此,实数![]() 的取值范围是
的取值范围是![]() ;
;
(2)由(1)可知![]() ,
,![]() ,且
,且![]() ,
,
![]() ,
,![]() .
.
①若![]() ,则
,则![]() ,合乎题意;
,合乎题意;
②若![]() ,则
,则![]() ,
,![]() 且函数
且函数![]() 的单调递减区间为
的单调递减区间为![]() ,
,
![]() ,即
,即![]() ,即
,即![]() ,解得
,解得![]() ,此时
,此时![]() .
.
综上所述,![]() 的取值范围是
的取值范围是![]() .
.
![]() 函数
函数![]() 在区间
在区间![]() 上单调递增,
上单调递增,![]() ,即
,即![]() .
.
因此,实数![]() 的取值范围是
的取值范围是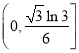 .
.

【题目】近年来,“无桩有站”模式的公共自行车日益普及,即传统自行车加装智能锁,实现扫码租车及刷卡租车、某公司量产了甲、乙两种款式的公共自行车并投人使用,为了调查消费者对两种自行车的租赁情况,现随机抽取这两种款式的自行车各100辆,分别统计了每辆车在某周内的出租次数,得到甲、乙两种自行车这周内出租次数的频数分布表:
甲 | |||||
出租次数(单位:次) |
|
|
|
|
|
频数 | 10 | 10 | 60 | 15 | 5 |
乙 | |||||
出租次数(单位:次) |
|
|
|
|
|
频数 | 20 | 25 | 25 | 10 | 20 |
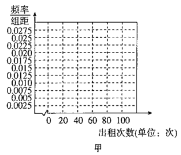
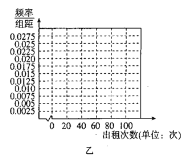
(1)根据频数分布表,完成上面频率分布直方图,并根据频率分布直方图比较甲、乙两种自行车这周内出租次数方差的大小(不必说明理由);
(2)如果两种自行车每次出租获得的利润相同,该公司决定大批量生产其中一种投入某城市使用,请你根据所学的统计知识,给出建议应该生产哪一种自行车,并说明你的理由.
【题目】2020年,北京将实行新的高考方案.新方案规定:语文数学和英语是考生的必考科目,考生还需从物理化学生物历史地理和政治六个科目中选取三个科目作为选考科目.若一个学生从六个科目中选出了三个科目作为选考科目,则称该学生的选考方案确定;否则,称该学生选考方案待确定,例如,学生甲选择“物理化学和生物”三个选考科目,则学生甲的选考方案确定,“物理化学和生物”为其选考方案.
某校为了解高一年级840名学生选考科目的意向,随机选取60名学生进行了一次调查,统计选考科目人数如下表:
性别 | 选考方案确定情况 | 物理 | 化学 | 生物 | 历史 | 地理 | 政治 |
男生 | 选考方案确定的有16人 | 16 | 16 | 8 | 4 | 2 | 2 |
选考方案待确定的有12人 | 8 | 6 | 0 | 2 | 0 | 0 | |
女生 | 选考方案确定的有20人 | 6 | 10 | 20 | 16 | 2 | 6 |
选考方案待确定的有12人 | 2 | 8 | 10 | 0 | 0 | 2 |
(1)估计该学校高一年级选考方案确定的学生中选考生物的学生有多少人?
(2)从选考方案确定的16名男生中随机选出2名,求恰好有一人选“物理化学生物”的概率;
(3)从选考方案确定的16名男生中随机选出2名,设随机变量 ,求
,求![]() 的分布列和期望.
的分布列和期望.