题目内容
已知p>0,q>0,p,q的等差中项是
,x=p+
,y=q+
,则x+y的最小值为( )
| 1 |
| 2 |
| 1 |
| p |
| 1 |
| q |
| A.3 | B.4 | C.5 | D.6 |
由题意可得由p,q的等差中项是
得,p+q=1,∵p>0,q>0,
∴x+y=p+
+q+
=p+q+
+
=3+
+
≥3+2=5,当且仅当
=
,即p=q=
时,取等号,
故x+y的最小值为5,
故选:C.
| 1 |
| 2 |
∴x+y=p+
| 1 |
| p |
| 1 |
| q |
| p+q |
| p |
| p+q |
| q |
| q |
| p |
| p |
| q |
| p |
| q |
| q |
| p |
| 1 |
| 2 |
故x+y的最小值为5,
故选:C.

练习册系列答案
相关题目
 是公差为
是公差为 的等差数列,
的等差数列, 是公比为
是公比为 的等比数列.
的等比数列. ,是否存在
,是否存在 ,有
,有 说明理由;
说明理由; ,
, ,并说明理由;
,并说明理由; 试确定所有的
试确定所有的 ,使数列
,使数列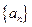 中,
中,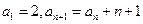 ,则通项
,则通项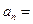 ___________。
___________。