题目内容
数列{an}中,Sn是前n项的和,且Sn=2an-3n
(1)求an
(2){an}中是否存在三项,使它们构成等差数列?若存在,求出这三项,若不存在,说明理由.
(1)求an
(2){an}中是否存在三项,使它们构成等差数列?若存在,求出这三项,若不存在,说明理由.
(1)∵Sn=2an-3n,
∴当n≥2时,Sn-1=2an-1-3(n-1),
∴Sn-Sn-1=(2an-3n)-[2an-1-3(n-1)],即an=2an-1+3,
∴an+3=2(an-1+3),
∴
=2(n≥2),
又a1=S1=2a1-3,解得a1=3,
∴数列{an+3}是首项为6,公比为2的等比数列,
∴an+3=6•2n-1=3•2n,
∴an=3•2n-3;
(2)设存在s,p,r∈N*,且s<p<r,使得as,ap,ar成等差数列,
∴2ap=as+ar,
∴2(3•2p-3)=3•2s-3+3•2r-3,
∴2p+1=2s+2r,2p-s+1=1+2r-s,2p-s+1,2r-s为偶数,
又∵1+2r-s为奇数,
∴2p+1=2s+2r不成立,
∴不存在满足条件的三项,
故{an}中不存在三项,使它们构成等差数列.
∴当n≥2时,Sn-1=2an-1-3(n-1),
∴Sn-Sn-1=(2an-3n)-[2an-1-3(n-1)],即an=2an-1+3,
∴an+3=2(an-1+3),
∴
| an+3 |
| an-1+3 |
又a1=S1=2a1-3,解得a1=3,
∴数列{an+3}是首项为6,公比为2的等比数列,
∴an+3=6•2n-1=3•2n,
∴an=3•2n-3;
(2)设存在s,p,r∈N*,且s<p<r,使得as,ap,ar成等差数列,
∴2ap=as+ar,
∴2(3•2p-3)=3•2s-3+3•2r-3,
∴2p+1=2s+2r,2p-s+1=1+2r-s,2p-s+1,2r-s为偶数,
又∵1+2r-s为奇数,
∴2p+1=2s+2r不成立,
∴不存在满足条件的三项,
故{an}中不存在三项,使它们构成等差数列.

练习册系列答案
相关题目
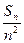 ,如果存在正整数M,使得对一切正整数n,Tn≤M都成立.则M的最小值是__________.
,如果存在正整数M,使得对一切正整数n,Tn≤M都成立.则M的最小值是__________.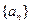 的前
的前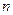 项和为
项和为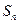 ,若
,若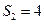 ,
,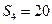 ,则该数列的公差
,则该数列的公差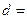 ( )
( )