题目内容
15.在△ABC中,角A,B,C所对的边分别为a,b,c,且(b-$\sqrt{2}c$)cosA+acosB=0.(1)求角A,
(2)若a=$\sqrt{10}$,cosB=$\frac{2\sqrt{5}}{5}$,D为AC的中点,求BD的长度.
分析 (1))△ABC中,由acosB=($\sqrt{2}$c-b)cosA,利用正弦定理求得cosA=$\frac{\sqrt{2}}{2}$,可得A的值.
(2)△ABC中,先由正弦定理求得AC的值,再由余弦定理求得AB的值,△ABD中,由余弦定理求得BD的值.
解答 解:(1)△ABC中,由acosB=($\sqrt{2}$c-b)cosA,利用正弦定理可得sinAcosB=$\sqrt{2}$sinCcosA-sinBcosA,
化简可得 sin(A+B)=$\sqrt{2}$sinCcosA,即 sinC=$\sqrt{2}$sinCcosA,求得cosA=$\frac{\sqrt{2}}{2}$,
∴A=$\frac{π}{4}$.
(2)由cosB=$\frac{2\sqrt{5}}{5}$,可得sinB=$\frac{\sqrt{5}}{5}$,再由正弦定理可得$\frac{a}{sinA}=\frac{b}{sinB}$,即$\frac{\sqrt{10}}{\frac{\sqrt{2}}{2}}=\frac{b}{\frac{\sqrt{5}}{5}}$,求得b=AC=2.
△ABC中,由余弦定理可得BC2=AB2+AC2-2AB•AC•cos∠A,即10=AB2+4-2AB•2•$\frac{\sqrt{2}}{2}$,求得AB=3$\sqrt{2}$.
△ABD中,由余弦定理可得 BD2=AB2+AD2-2AB•AD•cos∠A=18+1-6$\sqrt{2}$•$\frac{\sqrt{2}}{2}$=13,
∴BD=$\sqrt{13}$.
点评 本题主要考查正弦定理和余弦定理的应用,属于基本知识的考查.

练习册系列答案
相关题目
5.在△ABC中,若sin(A-B)=1+2cos(B+C)sin(A+C),则△ABC的形状一定是( )
| A. | 等边三角形 | B. | 不含60°的等腰三角形 | ||
| C. | 钝角三角形 | D. | 直角三角形 |
3.设a=0.82.1,b=21.1,c=log23,则( )
| A. | b<c<a | B. | c<a<b | C. | a<b<c | D. | a<c<b |
20.某几何体的三视图如图所示,则该几何体的体积为( )
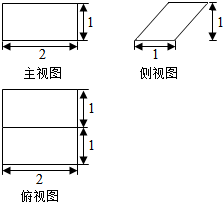

| A. | 1 | B. | 2 | C. | 2$\sqrt{2}$ | D. | $\frac{2}{3}$ |
7.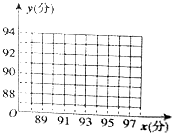 一次考试中,五名学生的数学、物理成绩如下表所示:
一次考试中,五名学生的数学、物理成绩如下表所示:
(1)要在这五名学生中选2名参加一项活动,求选中的同学中至少有一人的物理成绩高于90分的概率.
(2)根据上表数据,用变量y与x的相关系数和散点图说明物理成绩y与数学成绩x之间线性相关关系的强弱,如果具有较强的线性相关关系,求y与x的线性回归方程(系数精确到0.01);如果不具有线性相关关系,请说明理由.
参考公式:
相关系数r=$\frac{\sum_{i=1}^{n}{(x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sqrt{\sum_{i=1}^{n}({x}_{i-}\overline{x})^2\sum_{i=1}^{n}({y}_{i}-\overline{y})^2}}$
回归直线的方程:$\widehat{y}$=$\widehat{b}x+\widehat{a}$,其中$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^2}$,$\widehat{a}=\widehat{y}-\widehat{b}x$,$\widehat{{y}_{i}}$是与xi对应的回归估计值.
参考数据:$\overline{x}$=93,$\overline{y}$=90,$\sum_{i=1}^{n}{(x}_{i}-\overline{x})^2$=40,$\sum_{i=1}^{n}({y}_{i}-\overline{y})^2$=24,$\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})$=30,$\sqrt{40}$≈6.32,$\sqrt{24}$≈4.90.
 一次考试中,五名学生的数学、物理成绩如下表所示:
一次考试中,五名学生的数学、物理成绩如下表所示:| 学生 | A1 | A2 | A3 | A4 | A5 |
| 数学 | 89 | 91 | 93 | 95 | 97 |
| 物理 | 87 | 89 | 89 | 92 | 93 |
(2)根据上表数据,用变量y与x的相关系数和散点图说明物理成绩y与数学成绩x之间线性相关关系的强弱,如果具有较强的线性相关关系,求y与x的线性回归方程(系数精确到0.01);如果不具有线性相关关系,请说明理由.
参考公式:
相关系数r=$\frac{\sum_{i=1}^{n}{(x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sqrt{\sum_{i=1}^{n}({x}_{i-}\overline{x})^2\sum_{i=1}^{n}({y}_{i}-\overline{y})^2}}$
回归直线的方程:$\widehat{y}$=$\widehat{b}x+\widehat{a}$,其中$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^2}$,$\widehat{a}=\widehat{y}-\widehat{b}x$,$\widehat{{y}_{i}}$是与xi对应的回归估计值.
参考数据:$\overline{x}$=93,$\overline{y}$=90,$\sum_{i=1}^{n}{(x}_{i}-\overline{x})^2$=40,$\sum_{i=1}^{n}({y}_{i}-\overline{y})^2$=24,$\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})$=30,$\sqrt{40}$≈6.32,$\sqrt{24}$≈4.90.