题目内容
7.已知x2+y2-2ax-4ay+4a2=0,求证:(1)不论a取何值,上述圆的圆心在同一条直线上.
(2)不论a取何值,上述圆都有公切线,并求公切线方程.
分析 (1)将圆的方程化为标准方程,求得圆心和半径,令{x=ay=2a,则y=2x,即可得证;
(2)由于不论a取何值,上述圆的圆心在同一条直线y=2x上.又半径均为|a|,则存在两条公切线,且与直线y=2x平行,相距|a|;运用平行直线的距离公式,计算即可得到.
解答 证明:(1)圆x2+y2-2ax-4ay+4a2=0的标准方程为
(x-a)2+(y-2a)2=a2,
即有圆心为(a,2a),半径为|a|,(a≠0),
令{x=ay=2a,则y=2x,
故不论a取何值,上述圆的圆心在同一条直线y=2x上.
(2)由于不论a取何值,上述圆的圆心在同一条直线y=2x上.
又半径均为|a|,
则存在两条公切线,且与直线y=2x平行,相距|a|;
设公切线方程为y=2x+t,
由d=|t|√5=|a|,
解得t=±√5|a|,(a≠0),
即有两条公切线方程为y=2x+√5|a|,或y=2x-√5|a|,(a≠0).
点评 本题考查圆的一般式方程和标准方程的互化,圆的圆心和半径的求法,以及圆的公切线方程的求法,属于中档题.

练习册系列答案
相关题目
2.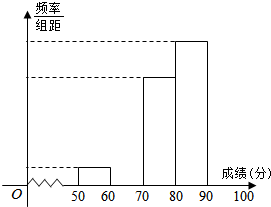 青少年“心理健康”问题越来越引起社会关注,某校对高一600名学生进行了一次“心理健康”知识测试,并从中抽取了部分学生的成绩(得分取正整数,满分100分)作为样本,绘制了下面尚未完成的频率分布表和频率分布直方图.
青少年“心理健康”问题越来越引起社会关注,某校对高一600名学生进行了一次“心理健康”知识测试,并从中抽取了部分学生的成绩(得分取正整数,满分100分)作为样本,绘制了下面尚未完成的频率分布表和频率分布直方图.
(1)填写答题卡上频率分布表中的空格,并补全频率分布直方图;
(2)试估计该年段成绩在[70,90)段的有多少人?
(3)请你估算该年段的平均分.
 青少年“心理健康”问题越来越引起社会关注,某校对高一600名学生进行了一次“心理健康”知识测试,并从中抽取了部分学生的成绩(得分取正整数,满分100分)作为样本,绘制了下面尚未完成的频率分布表和频率分布直方图.
青少年“心理健康”问题越来越引起社会关注,某校对高一600名学生进行了一次“心理健康”知识测试,并从中抽取了部分学生的成绩(得分取正整数,满分100分)作为样本,绘制了下面尚未完成的频率分布表和频率分布直方图.(1)填写答题卡上频率分布表中的空格,并补全频率分布直方图;
(2)试估计该年段成绩在[70,90)段的有多少人?
(3)请你估算该年段的平均分.
| 分组 | 频数 | 频率 |
| [50,60) | 2 | 0.04 |
| [60,70) | 8 | 0.16 |
| [70,80) | 10 | |
| [80,90) | ||
| [90,100] | 14 | 0.28 |
| 合计 | 1.00 |
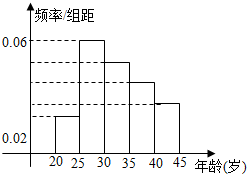 某居民小区年龄在20岁到45岁的居民共有150人,如图是他们上网情况的频率分布直方图,现已知年龄在[30,35),[40,45]的人数分别是39、21人,则年龄在[35,40)的频数( )
某居民小区年龄在20岁到45岁的居民共有150人,如图是他们上网情况的频率分布直方图,现已知年龄在[30,35),[40,45]的人数分别是39、21人,则年龄在[35,40)的频数( )