题目内容
10.已知集合A={x|x2+3x+2≤0},B={x|x2+ax+b≤0}.(Ⅰ)若(∁RA)∩B={x|-1<x≤2},(∁RA)∪B=R,求a,b的值;
(Ⅱ)若b=1,且A∪B=A,求实数a的取值范围.
分析 (Ⅰ)根据集合A,求得集合A,由(∁RA)∩B={x|-1<x≤2},(∁RA)∪B=R,求出集合B,根据不等式的解集与方程根之间的关系,利用韦达定理即可求得a,b的值,从而求得结果;
(Ⅱ)由A∪B=A,得到B⊆A,分类讨论即可得到a的取值范围.
解答 解:(Ⅰ)∵A={x|x2+3x+2≤0}=[-2,-1],
∴(∁RA)=(-∞,-2)∪(-1,+∞),
∵(∁RA)∩B={x|-1<x≤2}=(-1,2],(∁RA)∪B=R,
∴B=[-2,2],
∴-2+2=a,-2×2=b,
∴a=0,b=-4;
(Ⅱ)当b=1时,设f(x)=x2+ax+1,
∵A∪B=A,
∴B⊆A,
当B=∅时,由△=a2-4<0,解得-2<a<2,
当B≠∅时,由△=a2-4=0,解得a=-2,或a=2,
当a=-2时,B={1}不合题意,
当a=2时,B={-1}符合题意,
若△=a2-4>0,则$\left\{\begin{array}{l}{△>0}\\{f(-1)≥0}\\{f(-2)≥0}\\{-2≤-\frac{a}{2}≤-1}\end{array}\right.$,无解,
综上,所求实数a的范围为(-2,2].
点评 本题考查了集合的混合运算,对于一元二次不等式的求解,根据已知A∪B和A∩B的范围,求出集合B是解题的关键,属中档题

练习册系列答案
相关题目
20. 把正整数按一定的规律排成了如图所示的三角形数,设aij(i,j∈N+)是位于这个三角形数中从上往下数第i行,从左往右数第j列的数,如a32=5,若aij=2015,则i+j=( )
把正整数按一定的规律排成了如图所示的三角形数,设aij(i,j∈N+)是位于这个三角形数中从上往下数第i行,从左往右数第j列的数,如a32=5,若aij=2015,则i+j=( )
 把正整数按一定的规律排成了如图所示的三角形数,设aij(i,j∈N+)是位于这个三角形数中从上往下数第i行,从左往右数第j列的数,如a32=5,若aij=2015,则i+j=( )
把正整数按一定的规律排成了如图所示的三角形数,设aij(i,j∈N+)是位于这个三角形数中从上往下数第i行,从左往右数第j列的数,如a32=5,若aij=2015,则i+j=( )| A. | 111 | B. | 110 | C. | 108 | D. | 105 |
5.某几何体的三视图如图,则该几何体的体积为( )


| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | 2 | D. | 3 |
2.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$均为单位向量,其夹角为θ,给出命题:p:|$\overrightarrow{a}$-$\overrightarrow{b}$|>1;q:θ∈[$\frac{π}{2}$,$\frac{5π}{6}$),则p是q的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
2.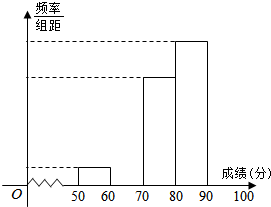 青少年“心理健康”问题越来越引起社会关注,某校对高一600名学生进行了一次“心理健康”知识测试,并从中抽取了部分学生的成绩(得分取正整数,满分100分)作为样本,绘制了下面尚未完成的频率分布表和频率分布直方图.
青少年“心理健康”问题越来越引起社会关注,某校对高一600名学生进行了一次“心理健康”知识测试,并从中抽取了部分学生的成绩(得分取正整数,满分100分)作为样本,绘制了下面尚未完成的频率分布表和频率分布直方图.
(1)填写答题卡上频率分布表中的空格,并补全频率分布直方图;
(2)试估计该年段成绩在[70,90)段的有多少人?
(3)请你估算该年段的平均分.
 青少年“心理健康”问题越来越引起社会关注,某校对高一600名学生进行了一次“心理健康”知识测试,并从中抽取了部分学生的成绩(得分取正整数,满分100分)作为样本,绘制了下面尚未完成的频率分布表和频率分布直方图.
青少年“心理健康”问题越来越引起社会关注,某校对高一600名学生进行了一次“心理健康”知识测试,并从中抽取了部分学生的成绩(得分取正整数,满分100分)作为样本,绘制了下面尚未完成的频率分布表和频率分布直方图.(1)填写答题卡上频率分布表中的空格,并补全频率分布直方图;
(2)试估计该年段成绩在[70,90)段的有多少人?
(3)请你估算该年段的平均分.
| 分组 | 频数 | 频率 |
| [50,60) | 2 | 0.04 |
| [60,70) | 8 | 0.16 |
| [70,80) | 10 | |
| [80,90) | ||
| [90,100] | 14 | 0.28 |
| 合计 | 1.00 |