题目内容
【题目】已知椭圆C:![]() =1(a>b>0)的左焦点分别为F1(-c,0),F2(c,0),过F2作垂直于x轴的直线l交椭圆C于A、B两点,满足|AF2|=
=1(a>b>0)的左焦点分别为F1(-c,0),F2(c,0),过F2作垂直于x轴的直线l交椭圆C于A、B两点,满足|AF2|=![]() c.
c.
(1)椭圆C的离心率;
(2)M、N是椭圆C短轴的两个端点,设点P是椭圆C上一点(异于椭圆C的顶点),直线MP、NP分别和x轴相交于R、Q两点,O为坐标原点,若|OR||OQ|=4,求椭圆C的方程.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】
试题(Ⅰ)法一:把![]() 点横坐标代入椭圆求得
点横坐标代入椭圆求得![]() ,从而得到
,从而得到![]() 的关系式,进而求得离心率;法二:直角
的关系式,进而求得离心率;法二:直角![]() 中,由勾股定理得到
中,由勾股定理得到![]() 的关系式,从而求得离心率;(Ⅱ)设
的关系式,从而求得离心率;(Ⅱ)设![]() ,则由
,则由![]() 、
、![]() 的方程中分别令
的方程中分别令![]() 得到
得到![]() 与
与![]() 点横坐标,从而由
点横坐标,从而由![]() 求得
求得![]() 的值,进而求出
的值,进而求出![]() 值,得到椭圆方程.
值,得到椭圆方程.
试题解析:(Ⅰ)法一:![]() 点横坐标为
点横坐标为![]() ,代入椭圆得
,代入椭圆得![]() ,
,
解得![]() ,∴
,∴![]() .
.
即![]() ,设
,设![]() ,∴
,∴![]() ,解得
,解得![]() .
.
法二:直角![]() 中,
中,![]() ,
,
∴由勾股定理得![]() ,即
,即![]() ,
,
∴![]() ,∴
,∴![]() ,即
,即![]()
(Ⅱ)设![]() ,
,
则![]() 方程为
方程为![]() ,令
,令![]() 得到
得到![]() 点横坐标为
点横坐标为![]() ;
;
![]() 方程为
方程为![]() ,令
,令![]() 得到
得到![]() 点横坐标为
点横坐标为![]() ;
;
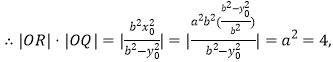
∴![]() ,∴椭圆
,∴椭圆![]() 的方程为
的方程为![]() .
.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
【题目】某校为了推动数学教学方法的改革,学校将高一年级部分生源情况基本相同的学生分成甲乙两个班,每班各40人,甲班按原有模式教学,乙班实施教学方法改革.经过一年的教学实验,将甲乙两个班学生一年来的数学成绩取平均数,两个班学生的平均成绩均在![]() ,按照区间
,按照区间![]() ,
,![]() ,
,![]() 进行分组,绘制成如下频率分布直方图,规定不低于80分(百分制)为优秀.
进行分组,绘制成如下频率分布直方图,规定不低于80分(百分制)为优秀.
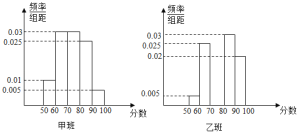
(1)完成表格,并判断是否有90%以上的把握认为“数学成绩优秀与教学改革有关”;
甲班 | 乙班 | 总计 | |
大于等于80分的人数 | |||
小于80分的人数 | |||
总计 |
(2)从乙班![]() 分数段中,按分层抽样随机抽取7名学生座谈,从中选三位同学发言,记来自
分数段中,按分层抽样随机抽取7名学生座谈,从中选三位同学发言,记来自![]() 发言的人数为随机变量
发言的人数为随机变量![]() ,求
,求![]() 的分布列和期望.附:
的分布列和期望.附: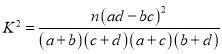 ,
,
| 0.10 | 0.05 | 0.025 |
| 2.706 | 3.841 | 5.024 |