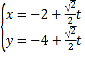题目内容
【题目】若对于任意x∈[1,4],不等式0≤ax2+bx+4a≤4x恒成立,|a|+|a+b+25|的范围为_____.
【答案】[25,57]
【解析】
先把不等式变形为﹣b≤a(x![]() )≤4﹣b恒成立,结合f(x)=x
)≤4﹣b恒成立,结合f(x)=x![]() 最值,找到
最值,找到![]() 的限制条件,结合线性规划的知识可得.
的限制条件,结合线性规划的知识可得.
对于任意x∈[1,4],不等式0≤ax2+bx+4a≤4x恒成立,
可得当x∈[1,4]时,不等式﹣b≤a(x![]() )≤4﹣b恒成立,
)≤4﹣b恒成立,
设f(x)=x![]() ,x∈[1,4];
,x∈[1,4];
可得x∈[1,2]时f(x)递减,x∈[2,4]时f(x)递增,
可得![]() 时取得最小值4,
时取得最小值4,![]() 或
或![]() 时取得最大值5,
时取得最大值5,
所以f(x)的值域为[4,5];
所以原不等式恒成立,等价于![]() ,
,
即![]() ,
,
设![]() ,则
,则![]() ,
,
所以![]() ,
,
所以目标函数z=|a|+|a+b+25|=|y﹣x|+|4x+3y+25|=|y﹣x|+4x+3y+25,
当y≥x时,目标函数z=3x+4y+25,
画出不等式组表示的平面区域,如图,
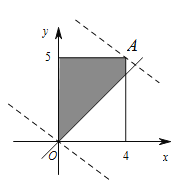
由图可知x=0,y=0时zmin=25,x=4,y=5时zmax=57;
当y<x时,目标函数z=5x+2y+25,如图,

由图可知x=0,y=0时zmin=25,x=4,y=4时zmax=53;
综上可得,|a|+|a+b+25|的范围是[25,57].

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目