题目内容
【题目】已知椭圆![]() 的四个顶点组成的四边形的面积为
的四个顶点组成的四边形的面积为![]() ,且经过点
,且经过点 .
.

(1)求椭圆![]() 的方程;
的方程;
(2)若椭圆![]() 的下顶点为
的下顶点为![]() ,如图所示,点
,如图所示,点![]() 为直线
为直线![]() 上的一个动点,过椭圆
上的一个动点,过椭圆![]() 的右焦点
的右焦点![]() 的直线
的直线![]() 垂直于
垂直于![]() ,且与
,且与![]() 交于
交于![]() 两点,与
两点,与![]() 交于点
交于点![]() ,四边形
,四边形![]() 和
和![]() 的面积分别为
的面积分别为![]() .求
.求![]() 的最大值.
的最大值.
【答案】(1)![]() (2)
(2)![]()
【解析】
试题分析:(1)由椭圆几何条件得椭圆四个顶点组成的四边形为菱形,其面积为![]() ,又
,又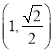 在椭圆
在椭圆![]() 上,所以
上,所以![]() ,解方程组得
,解方程组得![]() (2)先确定面积计算方法:
(2)先确定面积计算方法:![]() ,
,![]() ,再确定计算方向:设
,再确定计算方向:设![]() 根据两点间距离公式求OM,根据两直线交点求N点横坐标,再根据直线方程与椭圆方程联立方程组,结合韦达定理求弦长AB,最后根据
根据两点间距离公式求OM,根据两直线交点求N点横坐标,再根据直线方程与椭圆方程联立方程组,结合韦达定理求弦长AB,最后根据![]() 表达式形式,确定求最值方法(基本不等式求最值)
表达式形式,确定求最值方法(基本不等式求最值)
试题解析:(1)因为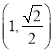 在椭圆
在椭圆![]() 上,所以
上,所以![]() ,
,
又因为椭圆四个顶点组成的四边形的面积为![]() ,所以
,所以![]() ,
,
解得![]() ,所以椭圆
,所以椭圆![]() 的方程为
的方程为![]() .
.
(2)由(1)可知![]() ,设
,设![]() ,
,
则当![]() 时,
时,![]() ,所以
,所以![]() ,
,
直线![]() 的方程为
的方程为![]() ,即
,即![]() ,
,
由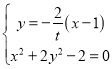 得
得![]() ,
,
则![]() ,
,
![]() ,
,
![]() ,
,
又![]() ,所以
,所以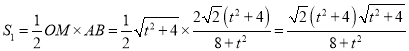 ,
,
由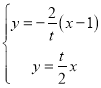 ,得
,得![]() ,所以
,所以![]() ,
,
所以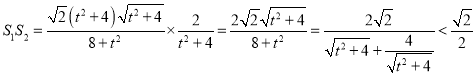 ,
,
当![]() 时,直线
时,直线![]() ,
,
所以当![]() 时,
时,![]() .
.

练习册系列答案
相关题目
【题目】在一次文、理学习倾向的调研中,对高一年段1000名学生进行文综、理综各一次测试(满分均为300分).测试后,随机抽取若干名学生成绩,记理综成绩为![]() ,文综成绩为
,文综成绩为![]() ,
,![]() 为
为![]() ,将
,将![]() 值分组统计制成下表:
值分组统计制成下表:
分组 | [0,20) | [20,40) | [40,60) | [60,80) | [80,100) | [100,120) | [120,140] |
频数 | 4 | 18 | 42 | 66 | 48 | 20 | 2 |
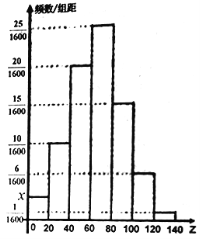
并将其中女生的![]() 值分布情况制成频率分布直方图(如图所示).
值分布情况制成频率分布直方图(如图所示).
(1)若已知直方图中[60,80)频数为25,试分别估计全体学生中,![]() 的男、女生人数;
的男、女生人数;
(2)记![]() 的平均数为
的平均数为![]() ,如果
,如果![]() 称为整体具有学科学习倾向,试估计高一年段女生的
称为整体具有学科学习倾向,试估计高一年段女生的![]() 值(同一组中的数据用该组区间中点值作代表),并判断高一年段女生是否整体具有显著学科学习倾向.
值(同一组中的数据用该组区间中点值作代表),并判断高一年段女生是否整体具有显著学科学习倾向.