题目内容
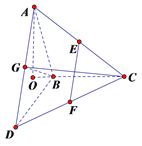
【题目】如图, ![]() 和
和![]() 所在平面互相垂直,且
所在平面互相垂直,且![]() ,
, ![]() 分别为AC、DC、AD的中点
分别为AC、DC、AD的中点

(1)求证: ![]() 平面BCG;
平面BCG;
(2)求三棱锥D-BCG的体积.
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:()根据等腰三角形三线合一的性质,利用中点得垂直,再根据中位线的性质即可证出;(2)作出![]() ,交
,交![]() 的延长线于O,可证明
的延长线于O,可证明![]()
![]() 平面
平面![]() ,又G为AD的中点,故可求出三棱锥的高,底面积根据面积公式求出即可.
,又G为AD的中点,故可求出三棱锥的高,底面积根据面积公式求出即可.
试题解析:(1)由已知得, ![]() 是
是![]() 的中位线,故
的中位线,故![]() ,
,
则可转化为证明![]() 平面BCG.易证
平面BCG.易证![]() ,
,
则有![]() ,则在等腰三角形
,则在等腰三角形![]() 和等腰三角形
和等腰三角形![]() 中,
中, ![]() 是
是![]() 中点,
中点,
故![]() ,
, ![]() .从而
.从而![]() 平面BCG,进而
平面BCG,进而![]() 平面BCG;
平面BCG;
(2)在平面![]() 内,作
内,作![]() ,交
,交![]() 的延长线于O,由平面
的延长线于O,由平面![]()
![]() 平面
平面![]() ,
,
知![]()
![]() 平面
平面![]() .又∵ G为AD的中点,因此G到平面BCD的距离
.又∵ G为AD的中点,因此G到平面BCD的距离
![]() 是AO长度的一半;在
是AO长度的一半;在![]() 中,
中, ![]() ;
;
∴![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目