题目内容
15.设函数f(x)的定义域为R,对任意实数x、y都有f(x+y)=f(x)+f(y),当x>0时f(x)<0且f(3)=-4.(1)证明:函数f(x)为奇函数;
(2)证明:函数f(x)在(-∞,+∞)上为减函数.
(3)求f(x)在区间[-9,9]上的最大值与最小值.
分析 (1)由已知中对于任意实数x,y都有f(x+y)=f(x)+f(y)成立,我们可以得到设x=y=0,则f(0)=0,再令y=-x可得f(-x)=-f(x),进而根据函数奇偶性的定义得到结论f(x)为奇函数,
(2)再利用函数单调性的定义由x>0时,有f(x)>0,结合对于任意实数x,y都有f(x+y)=f(x)+f(y)成立,判断出函数的单调性,
(3)根据单调性,以及f(3)=-4,得到f(x)在[-9,9]上有最大值和最小值.
解答 (1)证明:令x=y=0知f(0)=0,
令x+y=0知f(x)+f(-x)=0,
∴f(x)为奇函数.
(2)证明:任取两个自变量x1,x2且-∞<x1<x2<+∞,
则f(x2)-f(x1)=f(x2-x1),
∵x2>x1,∴x2-x1>0知f(x2-x1)<0,即f(x2)-f(x1)<0,
故f(x2)<f(x1),
∴f(x)在(-∞,+∞)上是减函数.
(3)解:∵f(x)在(-∞,+∞)上是减函数
∴f(x)在[-9,9]上有最大值和最小值
最小值为f(9)=f(6)+f(3)=f(3)+f(3)+f(3)=3f(3)=-12;
最大值为f(-9)=-f(9)=12.
点评 本题考查的知识点是抽象函数,函数单调性与性质,是对函数性质及应用的综合考查,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.如果实数x,y满足x2+y2=4,那么$\frac{y-2}{x+3}$的最小值是( )
| A. | -$\frac{12}{5}$ | B. | -1 | C. | -$\frac{5}{12}$ | D. | 0 |
20.下列各图中,可表示函数y=f(x)的图象的只可能是( )
| A. | 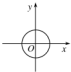 | B. | 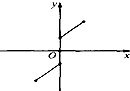 | C. | 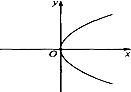 | D. | 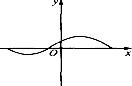 |
7.已知$a={log_3}\frac{1}{2},b={2^{0.01}},c=ln\frac{1}{2}$,则a,b,c的大小关系为( )
| A. | b>a>c | B. | b>c>a | C. | a>c>b | D. | a>b>c |
 设全集为U=R,集合A={x|(x+3)(x-6)≤0},B={x|log2(x+2)<4}.
设全集为U=R,集合A={x|(x+3)(x-6)≤0},B={x|log2(x+2)<4}.