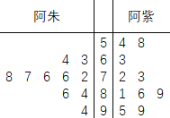
��Ŀ����
����Ŀ����ȱ����У�![]() ���Ĺ���Ϊ q(q > 0��q = 1)��ǰ n ���Ϊ Sn���� 2a1a3 = a4�����У�
���Ĺ���Ϊ q(q > 0��q = 1)��ǰ n ���Ϊ Sn���� 2a1a3 = a4�����У�![]() ����ǰ n ��� Tn ����2Tn = n(bn - 1)��n ��N����b2 = 1.
����ǰ n ��� Tn ����2Tn = n(bn - 1)��n ��N����b2 = 1.
(1) ������ ��![]() ������
������![]() ����ͨ�ʽ��
����ͨ�ʽ��
(2) �Ƿ���ڳ��� t��ʹ�� {Sn+ ![]() } Ϊ�ȱ����У�˵�����ɣ�
} Ϊ�ȱ����У�˵�����ɣ�
(3) �� cn =![]() ��������������������� k(k ��2), �Ƿ���������� l��m(k < l < m), ʹ�� ck��c1��cm �ɵȲ����У������ڣ���� l��m���� k ��ʾ�����������ڣ�˵������.
��������������������� k(k ��2), �Ƿ���������� l��m(k < l < m), ʹ�� ck��c1��cm �ɵȲ����У������ڣ���� l��m���� k ��ʾ�����������ڣ�˵������.
���𰸡���1��![]() �� ��2������
�� ��2������![]() ��ʹ��
��ʹ��![]() �ǹ���Ϊ
�ǹ���Ϊ![]() �ĵȱ����У���3������
�ĵȱ����У���3������![]() ��������.
��������.
��������
��1�����û���������ɵ�![]() ������n��2ʱ��2bn��2��Tn��Tn��1���������ɵ�
������n��2ʱ��2bn��2��Tn��Tn��1���������ɵ�![]() ��
��
��2����Sn![]() ���ֱ�����t
���ֱ�����t![]() ʱ��t
ʱ��t![]() ʱ���ɵȱ����еĶ���֤�����ɣ�
ʱ���ɵȱ����еĶ���֤�����ɣ�
��3������������������������k��k��2��������������l��m��k��l��m����ʹ��ck��c1��cm�ɵȲ����У���![]() �������ã�2m+1
�������ã�2m+1![]() ��ȡl��2k�����ɵý�.
��ȡl��2k�����ɵý�.
��1���ȱ�����{an}�Ĺ���Ϊq��q��0��q��1������2a1a3��a4��
��![]() ���ɵ�a1
���ɵ�a1![]() ��
��
��an![]() qn��1
qn��1![]() ��
��
����{bn}��ǰn���Tn����2Tn��n��bn��1����n��N*��b2��1��
��n��2ʱ��2bn��2��Tn��Tn��1����n��bn��1������n��1����bn��1��1����
������n��2��bn����n��1��bn��1+1��
��n��3ʱ������ͬ���ԣ�n��2����n��1�����ɵã�![]() ��
��
�����ۼ���Ϳɵã�![]() b2+1
b2+1![]() ������bn��2n��3��n��3����
������bn��2n��3��n��3����
��n��1ʱ��2b1��b1��1�����b1����1��
������֤n��1��2ʱҲ���㣮
��bn��2n��3��
��2���ɣ�1����֪��an![]() ��q��0��q��1��
��q��0��q��1��
��Sn![]() ��
��
����t![]() ʱ����Sn
ʱ����Sn![]() ����
���� q��
q��
������{Sn![]() }�ǹ���Ϊq�ĵȱ����У�
}�ǹ���Ϊq�ĵȱ����У�
����t![]() ʱ����Sn
ʱ����Sn![]() ��
��
��![]() A��
A��![]() B��������A��B��0����
B��������A��B��0����
��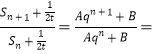 q
q![]() ��������
��������
���ϣ�����t![]() ʱ��ʹ������{Sn
ʱ��ʹ������{Sn![]() }�ǹ���Ϊq�ĵȱ����У�
}�ǹ���Ϊq�ĵȱ����У�
��3���ɣ�1����֪��bn��2n��3��
![]() ��
��
����������������������k��k��2��������������l��m��k��l��m����ʹ��ck��c1��cm�ɵȲ����У�
��![]() �������ã�2m+1
�������ã�2m+1![]() ��
��
ȡl��2k����2m+1����4k+1����2k+1�������m��4k2+3k��
������l��2k��m��4k2+3k���������⣮

 ��˼ά������ҵ���ټ��ִ�ѧ������ϵ�д�
��˼ά������ҵ���ټ��ִ�ѧ������ϵ�д�����Ŀ����ȫ�濹���¹ڷ���������һ����ʱ�ڣ����н����������ͣ�β�ͣѧ���Ŀںţ�����ѧ������ѧϰ.ijУ��ѧ��ʦΪ�˵������ѧ����ѧ�ɼ�������ѧϰʱ��֮�����ع�ϵ���ڸ����꼶�����ѡȡ![]() ��ѧ�����и����ʾ�������ÿ������ѧϰ��ѧʱ�䲻����
��ѧ�����и����ʾ�������ÿ������ѧϰ��ѧʱ�䲻����![]() Сʱ����
Сʱ����![]() �ˣ�����
�ˣ�����![]() ���з�������
���з�������![]() �ֵ���
�ֵ���![]() �ˣ���ÿ������ѧϰ��ѧʱ�䲻����
�ˣ���ÿ������ѧϰ��ѧʱ�䲻����![]() Сʱ�����У��ڼ�⿼������ѧƽ���ɼ�����
Сʱ�����У��ڼ�⿼������ѧƽ���ɼ�����![]() �ֵ�ռ
�ֵ�ռ![]() .
.
��1�������![]() �����������ж��Ƿ���
�����������ж��Ƿ���![]() �İ�����Ϊ������ѧ������ѧ�ɼ���ѧ������ѧϰʱ���йء���
�İ�����Ϊ������ѧ������ѧ�ɼ���ѧ������ѧϰʱ���йء���
���������� | �������� | �ϼ� | |
����ѧϰʱ�䲻���� | |||
����ѧϰʱ�䲻�� | |||
�ϼ� |
��2�������������дӷ���������![]() �ֵ�ѧ���У����շֲ�����ķ������鵽����ѧϰʱ�䲻����
�ֵ�ѧ���У����շֲ�����ķ������鵽����ѧϰʱ�䲻����![]() Сʱ������ѧϰʱ�䲻��
Сʱ������ѧϰʱ�䲻��![]() Сʱ��ѧ����
Сʱ��ѧ����![]() ����������
����������![]() ��ѧ���������ȡ
��ѧ���������ȡ![]() �ˣ�����
�ˣ�����![]() ��ÿ������ѧϰʱ�䶼����
��ÿ������ѧϰʱ�䶼����![]() Сʱ�ĸ���.���ٽ�ֵ�������ο���
Сʱ�ĸ���.���ٽ�ֵ�������ο���
|
|
|
|
|
|
|
|
|
|
|
|
|
|
���ο���ʽ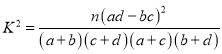 ������
������![]() ��
��
����Ŀ��Ϊ���и�����������ˮƽ.��ij����ͨ���е�ij�������У��ο����Ŀ���������������֮��Ϊ![]() ���ҳɼ��ֲ���
���ҳɼ��ֲ���![]() �ķ�Χ�ڣ��涨������50���ϣ���50�������ı���Ϊ���������ġ������������÷ֲ�����ķ�����ȡ400�˵ijɼ���Ϊ�������õ��ɼ���Ƶ�ʷֲ�ֱ��ͼ����ͼ��ʾ.����
�ķ�Χ�ڣ��涨������50���ϣ���50�������ı���Ϊ���������ġ������������÷ֲ�����ķ�����ȡ400�˵ijɼ���Ϊ�������õ��ɼ���Ƶ�ʷֲ�ֱ��ͼ����ͼ��ʾ.����![]() ������2Ϊ���ȵĵȱ�����.
������2Ϊ���ȵĵȱ�����.
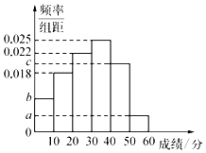
��1����![]() ��ֵ��
��ֵ��
��2����д����![]() ���������ܷ��ڷ�����ĸ��ʲ�����0.01���������Ϊ������������ġ��롰ѧ���������ơ��йأ�
���������ܷ��ڷ�����ĸ��ʲ�����0.01���������Ϊ������������ġ��롰ѧ���������ơ��йأ�
�Ŀ��� | ������ | �ϼ� | |
�� | 6 | ||
���� | |||
�ϼ� | 400 |
��3���������������õ�Ƶ����Ϊ���ʣ��ִ�ȫ�вο�ѧ���У������ȡ2��ѧ�����ǡ�����������ġ���ѧ������Ϊ![]() ����
����![]() �ķֲ��м���ѧ����.
�ķֲ��м���ѧ����.
����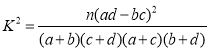 ������
������![]() .
.
| .15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |