题目内容
14.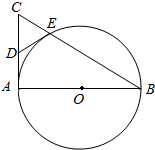 如图,AB是⊙O的直径,AC是⊙O的切线,BC交⊙O于点E.
如图,AB是⊙O的直径,AC是⊙O的切线,BC交⊙O于点E.(Ⅰ)若D为AC的中点,证明:DE是⊙O的切线;
(Ⅱ)若OA=$\sqrt{3}$CE,求∠ACB的大小.
分析 (Ⅰ)连接AE和OE,由三角形和圆的知识易得∠OED=90°,可得DE是⊙O的切线;
(Ⅱ)设CE=1,AE=x,由射影定理可得关于x的方程x2=$\sqrt{12-{x}^{2}}$,解方程可得x值,可得所求角度.
解答  解:(Ⅰ)连接AE,由已知得AE⊥BC,AC⊥AB,
解:(Ⅰ)连接AE,由已知得AE⊥BC,AC⊥AB,
在RT△ABC中,由已知可得DE=DC,∴∠DEC=∠DCE,
连接OE,则∠OBE=∠OEB,
又∠ACB+∠ABC=90°,∴∠DEC+∠OEB=90°,
∴∠OED=90°,∴DE是⊙O的切线;
(Ⅱ)设CE=1,AE=x,
由已知得AB=2$\sqrt{3}$,BE=$\sqrt{12-{x}^{2}}$,
由射影定理可得AE2=CE•BE,
∴x2=$\sqrt{12-{x}^{2}}$,即x4+x2-12=0,
解方程可得x=$\sqrt{3}$
∴∠ACB=60°
点评 本题考查圆的切线的判定,涉及射影定理和三角形的知识,属基础题.

练习册系列答案
相关题目
4.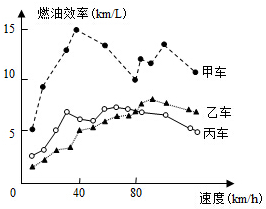 汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,如图描述了甲、乙、丙三辆汽车在不同速度下燃油效率情况,下列叙述中正确的是( )
汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,如图描述了甲、乙、丙三辆汽车在不同速度下燃油效率情况,下列叙述中正确的是( )
 汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,如图描述了甲、乙、丙三辆汽车在不同速度下燃油效率情况,下列叙述中正确的是( )
汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,如图描述了甲、乙、丙三辆汽车在不同速度下燃油效率情况,下列叙述中正确的是( )| A. | 消耗1升汽油,乙车最多可行驶5千米 | |
| B. | 以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多 | |
| C. | 甲车以80千米/小时的速度行驶1小时,消耗10升汽油 | |
| D. | 某城市机动车最高限速80千米/小时,相同条件下,在该市用丙车比用乙车更省油 |
4. 如图,在圆O中,M、N是弦AB的三等分点,弦CD,CE分别经过点M,N,若CM=2,MD=4,CN=3,则线段NE的长为( )
如图,在圆O中,M、N是弦AB的三等分点,弦CD,CE分别经过点M,N,若CM=2,MD=4,CN=3,则线段NE的长为( )
 如图,在圆O中,M、N是弦AB的三等分点,弦CD,CE分别经过点M,N,若CM=2,MD=4,CN=3,则线段NE的长为( )
如图,在圆O中,M、N是弦AB的三等分点,弦CD,CE分别经过点M,N,若CM=2,MD=4,CN=3,则线段NE的长为( )| A. | $\frac{8}{3}$ | B. | 3 | C. | $\frac{10}{3}$ | D. | $\frac{5}{2}$ |
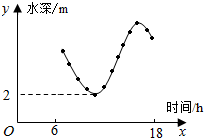 如图,某港口一天6时到18时的水深变化曲线近似满足函数y=3sin($\frac{π}{6}$x+φ)+k.据此函数可知,这段时间水深(单位:m)的最大值为( )
如图,某港口一天6时到18时的水深变化曲线近似满足函数y=3sin($\frac{π}{6}$x+φ)+k.据此函数可知,这段时间水深(单位:m)的最大值为( )