题目内容
3.一个圆经过椭圆$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{4}$=1的三个顶点.且圆心在x轴的正半轴上.则该圆标准方程为(x-$\frac{3}{2}$)2+y2=$\frac{25}{4}$.分析 利用椭圆的方程求出顶点坐标,然后求出圆心坐标,求出半径即可得到圆的方程.
解答  解:一个圆经过椭圆$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{4}$=1的三个顶点.且圆心在x轴的正半轴上.
解:一个圆经过椭圆$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{4}$=1的三个顶点.且圆心在x轴的正半轴上.
可知椭圆的右顶点坐标(4,0),上下顶点坐标(0,±2),
设圆的圆心(a,0),则$\sqrt{({a-0)}^{2}+(0-2)^{2}}=4-a$,解得a=$\frac{3}{2}$,
圆的半径为:$\frac{5}{2}$,
所求圆的方程为:(x-$\frac{3}{2}$)2+y2=$\frac{25}{4}$.
故答案为:(x-$\frac{3}{2}$)2+y2=$\frac{25}{4}$.
点评 本题考查椭圆的简单性质的应用,圆的方程的求法,考查计算能力.

练习册系列答案
相关题目
11.某企业生产甲、乙两种产品均需用A、B两种原料.已知生产1吨每种产品所需原料及每天原料的可用限额如表所示.如果生产一吨甲、乙产品可获得利润分别为3万元、4万元,则该企业每天可获得最大利润为( )
| 甲 | 乙 | 原料限额 | |
| A(吨) | 3 | 2 | 12 |
| B(吨) | 1 | 2 | 8 |
| A. | 12万元 | B. | 16万元 | C. | 17万元 | D. | 18万元 |
18.sin20°cos10°-cos160°sin10°=( )
| A. | $-\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $-\frac{1}{2}$ | D. | $\frac{1}{2}$ |
8.命题“?x0∈(0,+∞),lnx0=x0-1”的否定是( )
| A. | ?x0∈(0,+∞),lnx0≠x0-1 | B. | ?x0∉(0,+∞),lnx0=x0-1 | ||
| C. | ?x∈(0,+∞),lnx≠x-1 | D. | ?x∉(0,+∞),lnx=x-1 |
15.设变量x,y满足约束条件$\left\{{\begin{array}{l}{x+y≤4}\\{x-y≤2}\\{3x-y≥0}\end{array}}\right.$,则3x+y的最大值为10.
13.设复数z=(x-1)+yi(x,y∈R),若|z|≤1,则y≥x的概率为( )
| A. | $\frac{3}{4}$+$\frac{1}{2π}$ | B. | $\frac{1}{2}$+$\frac{1}{π}$ | C. | $\frac{1}{4}$-$\frac{1}{2π}$ | D. | $\frac{1}{2}$-$\frac{1}{π}$ |
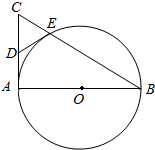 如图,AB是⊙O的直径,AC是⊙O的切线,BC交⊙O于点E.
如图,AB是⊙O的直径,AC是⊙O的切线,BC交⊙O于点E.