题目内容
19.在平面直角坐标系xOy中,已知向量$\overrightarrow{m}$=($\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$),$\overrightarrow{n}$=(sinx,cosx),x∈(0,$\frac{π}{2}$).(1)若$\overrightarrow{m}$⊥$\overrightarrow{n}$,求tanx的值;
(2)若$\overrightarrow{m}$与$\overrightarrow{n}$的夹角为$\frac{π}{3}$,求x的值.
分析 (1)若$\overrightarrow{m}$⊥$\overrightarrow{n}$,则$\overrightarrow{m}$•$\overrightarrow{n}$=0,结合三角函数的关系式即可求tanx的值;
(2)若$\overrightarrow{m}$与$\overrightarrow{n}$的夹角为$\frac{π}{3}$,利用向量的数量积的坐标公式进行求解即可求x的值.
解答 解:(1)若$\overrightarrow{m}$⊥$\overrightarrow{n}$,
则$\overrightarrow{m}$•$\overrightarrow{n}$=($\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$)•(sinx,cosx)=$\frac{\sqrt{2}}{2}$sinx-$\frac{\sqrt{2}}{2}$cosx=0,
即$\frac{\sqrt{2}}{2}$sinx=$\frac{\sqrt{2}}{2}$cosx
sinx=cosx,即tanx=1;
(2)∵|$\overrightarrow{m}$|=$\sqrt{(\frac{\sqrt{2}}{2})^{2}+(-\frac{\sqrt{2}}{2})^{2}}=\sqrt{\frac{1}{2}+\frac{1}{2}}=1$,|$\overrightarrow{n}$|=$\sqrt{sin^2x+cos^2x}$=1,$\overrightarrow{m}$•$\overrightarrow{n}$=($\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$)•(sinx,cosx)=$\frac{\sqrt{2}}{2}$sinx-$\frac{\sqrt{2}}{2}$cosx,
∴若$\overrightarrow{m}$与$\overrightarrow{n}$的夹角为$\frac{π}{3}$,
则$\overrightarrow{m}$•$\overrightarrow{n}$=|$\overrightarrow{m}$|•|$\overrightarrow{n}$|cos$\frac{π}{3}$=$\frac{1}{2}$,
即$\frac{\sqrt{2}}{2}$sinx-$\frac{\sqrt{2}}{2}$cosx=$\frac{1}{2}$,
则sin(x-$\frac{π}{4}$)=$\frac{1}{2}$,
∵x∈(0,$\frac{π}{2}$).
∴x-$\frac{π}{4}$∈(-$\frac{π}{4}$,$\frac{π}{4}$).
则x-$\frac{π}{4}$=$\frac{π}{6}$
即x=$\frac{π}{4}$+$\frac{π}{6}$=$\frac{5π}{12}$.
点评 本题主要考查向量数量积的定义和坐标公式的应用,考查学生的计算能力,比较基础.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案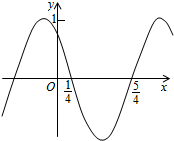
| A. | (kπ-$\frac{1}{4}$,kπ+$\frac{3}{4}$,),k∈z | B. | (2kπ-$\frac{1}{4}$,2kπ+$\frac{3}{4}$),k∈z | ||
| C. | (k-$\frac{1}{4}$,k+$\frac{3}{4}$),k∈z | D. | ($2k-\frac{1}{4}$,2k+$\frac{3}{4}$),k∈z |
| A. | [0,1] | B. | (0,1] | C. | [0,1) | D. | (-∞,1] |
| 甲 | 乙 | 原料限额 | |
| A(吨) | 3 | 2 | 12 |
| B(吨) | 1 | 2 | 8 |
| A. | 12万元 | B. | 16万元 | C. | 17万元 | D. | 18万元 |
| A. | ?x0∈(0,+∞),lnx0≠x0-1 | B. | ?x0∉(0,+∞),lnx0=x0-1 | ||
| C. | ?x∈(0,+∞),lnx≠x-1 | D. | ?x∉(0,+∞),lnx=x-1 |
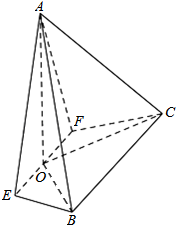 如图,在四棱锥A-EFCB中,△AEF为等边三角形,平面AEF⊥平面EFCB,EF∥BC,BC=4,EF=2a,∠EBC=∠FCB=60°,O为EF的中点.
如图,在四棱锥A-EFCB中,△AEF为等边三角形,平面AEF⊥平面EFCB,EF∥BC,BC=4,EF=2a,∠EBC=∠FCB=60°,O为EF的中点.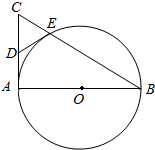 如图,AB是⊙O的直径,AC是⊙O的切线,BC交⊙O于点E.
如图,AB是⊙O的直径,AC是⊙O的切线,BC交⊙O于点E.