��Ŀ����
6��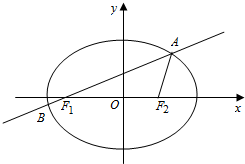 ��ͼ����֪��Բ$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1��{a��b��0}��$��������Ϊ$\frac{{\sqrt{2}}}{2}$��F1��F2Ϊ�����ҽ��㣬��F1��ֱ��l����Բ��A��B���㣬��F1AF2���ܳ�Ϊ$2��\sqrt{2}+1��$��
��ͼ����֪��Բ$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1��{a��b��0}��$��������Ϊ$\frac{{\sqrt{2}}}{2}$��F1��F2Ϊ�����ҽ��㣬��F1��ֱ��l����Բ��A��B���㣬��F1AF2���ܳ�Ϊ$2��\sqrt{2}+1��$����1������Բ�ı����̣�
��2�����AOB��������ֵ��OΪ����ԭ�㣩��
��3��ֱ��mҲ��F1��������Բ����C��D���㣬��l��m�����߶�AB��CD���е�ֱ�ΪM��N���㣬���ʣ�ֱ��MN�Ƿ�����㣿���ǣ�����������ꣻ�����ǣ���˵�����ɣ�
���� ��1������Բ�İ뽹��Ϊc�������������Լ���F1AF2���ܳ������a��c��Ȼ�������Բ�ı����̣�
��2����ֱ��l�ķ���Ϊ��x=ky-1����$\frac{x^2}{2}+{y^2}=1$��������x�������ã���k2+2��y2-2ky-1=0���A��B�������꣬��ʾ�������ε������ʽ������������ͨ����������ʽ�����ֵ��
��3��������$��{-\frac{2}{3}��0}��$��ͨ���������β��룬���ж��㣬����x ���ϣ���k��0��k�١�1������£���ֱ��l�ķ���Ϊ��x=ky-1��ֱ��m�ķ���Ϊ��$x=-\frac{1}{k}y-1$�����M���꣬�ɵ�ֱ��MN�ķ��̣�����ֱ��ϵ�Ƴ�������ɣ�
��� �⣺��1������Բ�İ뽹��Ϊc����$\frac{c}{a}=\frac{{\sqrt{2}}}{2}$��������֪ $2��{a+c}��=2��{\sqrt{2}+1}��$��
�����������$a=\sqrt{2}$��c=1����b2=1��������Բ�ı�����Ϊ$\frac{x^2}{2}+{y^2}=1$��������4�֣�
��2����ֱ��l�ķ���Ϊ��x=ky-1����$\frac{x^2}{2}+{y^2}=1$��������x�������ã���k2+2��y2-2ky-1=0����=��-2k��2+4��k2+2��=8k2+8��0��${y_1}=\frac{{2k+\sqrt{8{k^2}+8}}}{{2��{{k^2}+1}��}}$��${y_2}=\frac{{2k-\sqrt{8{k^2}+8}}}{{2��{{k^2}+1}��}}$������6�֣�
����${S_{��AOB}}={S_{��AOF}}+{S_{��BOF}}=\frac{1}{2}|{O{F_1}}||{{y_1}-{y_2}}|$=$\frac{1}{2}|{{y_1}-{y_2}}|$=$\frac{1}{2}\frac{{\sqrt{8{k^2}+8}}}{{{k^2}+2}}$=$\sqrt{2}\frac{{\sqrt{{k^2}+1}}}{{{k^2}+2}}$������7�֣�=$\sqrt{2}\sqrt{\frac{{{k^2}+1}}{{{{��{{k^2}+2}��}^2}}}}$=$\sqrt{2}\sqrt{\frac{{{k^2}+1}}{{{{[{��{{k^2}+1}��+1}]}^2}}}}$=$\sqrt{2}\sqrt{\frac{{{k^2}+1}}{{{{��{{k^2}+1}��}^2}+2��{{k^2}+1}��+1}}}$=$\sqrt{2}\sqrt{\frac{1}{{��{{k^2}+1}��+\frac{1}{{{k^2}+1}}+2}}}$$��\sqrt{2}\sqrt{\frac{1}{2+2}}=\frac{{\sqrt{2}}}{2}$�����ҽ���${k^2}+1=\frac{1}{{{k^2}+1}}$��
��k=0ʱ�Ⱥų����������ԡ�AOB��������ֵΪ$\frac{{\sqrt{2}}}{2}$������10�֣�
��3��������$��{-\frac{2}{3}��0}��$��ͨ���������β��룬���ж��㣬����x ���ϣ�
��k��0��k�١�1������£���ֱ��l�ķ���Ϊ��x=ky-1��
ֱ��m�ķ���Ϊ��$x=-\frac{1}{k}y-1$��
�ɣ�2���ã�${y_M}=\frac{{{y_1}+{y_2}}}{2}=\frac{k}{{{k^2}+2}}$��
��${x_M}=k\frac{k}{{{k^2}+2}}-1=\frac{-2}{{{k^2}+2}}$����$M��{\frac{-2}{{{k^2}+2}}��\frac{k}{{{k^2}+2}}}��$��
��$N��{\frac{{-2{k^2}}}{{2{k^2}+1}}��\frac{-k}{{2{k^2}+1}}}��$������12�֣�
�ɵ�ֱ��MN�ķ��̣�$y+\frac{k}{{2{k^2}+1}}=\frac{{\frac{k}{{{k^2}+2}}-\frac{-k}{{2{k^2}+1}}}}{{\frac{-2}{{{k^2}+2}}-\frac{{-2{k^2}}}{{2{k^2}+1}}}}��{x+\frac{{2{k^2}}}{{2{k^2}+1}}}��$��
��$y+\frac{k}{{2{k^2}+1}}=\frac{3k}{{2��{{k^2}-1}��}}��{x+\frac{{2{k^2}}}{{2{k^2}+1}}}��$����$y=\frac{3k}{{2��{{k^2}-1}��}}��{x+\frac{{2{k^2}}}{{2{k^2}+1}}}��-\frac{k}{{2{k^2}+1}}$$y=\frac{3k}{{2��{{k^2}-1}��}}[{x+\frac{{2{k^2}}}{{2{k^2}+1}}-\frac{k}{{2{k^2}+1}}•\frac{{2��{{k^2}-1}��}}{3k}}]$����$y=\frac{3k}{{2��{{k^2}-1}��}}��{x+\frac{2}{3}}��$��
��ֱ��MN������$��{-\frac{2}{3}��0}��$������y=0������$x=-\frac{2}{3}$��
����֤��k=0��k=��1ʱ�������Գ�����
���ϣ�ֱ��MN������$��{-\frac{2}{3}��0}��$����14�֣�
���� ���⿼��ֱ������Բ��λ�ù�ϵ���ۺ�Ӧ�ã���Բ���̵�����������ʽ����ֵ�е�Ӧ�ã������������������������Լ�����������

 ͬ����ϰǿ����չϵ�д�
ͬ����ϰǿ����չϵ�д�| A�� | -2 | B�� | 2 | C�� | 4 | D�� | -4 |
 ��ͼ������Բ$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1��{a��b��0}��$��һ��P��x�������ߣ�����ǡΪ��F1���ֵ�A����Բ��x ��������Ľ��㣬��B����Բ��y��������Ľ��㣬��AB��OP������Բ��������Ϊ��������
��ͼ������Բ$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1��{a��b��0}��$��һ��P��x�������ߣ�����ǡΪ��F1���ֵ�A����Բ��x ��������Ľ��㣬��B����Բ��y��������Ľ��㣬��AB��OP������Բ��������Ϊ��������| A�� | $\frac{1}{2}$ | B�� | $\frac{{\sqrt{5}}}{5}$ | C�� | $\frac{{\sqrt{2}}}{2}$ | D�� | $\frac{{\sqrt{3}}}{2}$ |
| A�� | {x|-2��x��3} | B�� | {x|-2��x��3} | C�� | {x|x��-2��x��3} | D�� | {x|-2��x��3} |
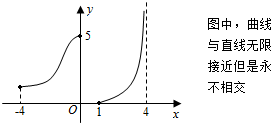
| A�� | ����f��x���Ķ�����Ϊ[-4��4�� | |
| B�� | ����f��x����ֵ��Ϊ[0��5] | |
| C�� | �˺����ڶ������ڼȲ���������Ҳ���Ǽ����� | |
| D�� | ���������y��[0��+�ޣ�������Ψһ���Ա���x��֮��Ӧ |
| A�� | ���������ݵõ��Ļع鷽��$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$�ع��������ģ�$\overline{x}$��$\overline{y}$�� | |
| B�� | �в�ƽ����ԽС��ģ�ͣ���ϵ�Ч��Խ�� | |
| C�� | �����ָ��R2���̻��ع�Ч����R2ԽС��˵��ģ�͵����Ч��Խ�� | |
| D�� | ����������������������Խǿ�����ϵ���ľ���ֵԽ�ӽ���1 |