题目内容
16.对两个变量y和x进行回归分析,得到一组样本数据:(x1,y1),(x2,y2),…,(xn,yn),则下列说法中不正确的是( )| A. | 由样本数据得到的回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$必过样本中心($\overline{x}$,$\overline{y}$) | |
| B. | 残差平方和越小的模型,拟合的效果越好 | |
| C. | 用相关指数R2来刻画回归效果,R2越小,说明模型的拟合效果越好 | |
| D. | 两个随机变量的线性相关性越强,相关系数的绝对值越接近于1 |
分析 对四个选项分别进行判断,即可得出结论.
解答 解:由样本数据得到的回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$必过样本中心($\overline{x}$,$\overline{y}$),正确;
残差平方和越小的模型,拟合的效果越好,正确
用相关指数R2来刻画回归效果,R2越大,说明模型的拟合效果越好,不正确,
线性相关系数|r|越大,两个变量的线性相关性越强,故正确.
故选:C.
点评 本题考查两个变量的线性相关和线性回归方程,用来描述拟合效果好坏的量比较多,注意各个量的区别,不要弄混.

练习册系列答案
相关题目
7.已知集合A={x|x2+y2=1},B={y|y=cos2x},则( )
| A. | A∩B={(0,1)} | B. | A=B | C. | A∩B=ϕ | D. | A∩B=B |
4.已知m,n是不同的直线,α,β,γ是不同的平面,下列命题中,正确的是( )
| A. | 若α⊥β,α∩β=m,m⊥n,则n⊥α,n⊥β | |
| B. | 若α∥β,α∩γ=m,β∩γ=n,则m∥n | |
| C. | 若m不垂直于α,则m不可能垂直于α内的无数条直线 | |
| D. | 若α∩β=m,n∥m,则n∥α,且n∥β |
1.设全集U={1,2,3,4,5,6,7,8},A={1,4,8},B={3,4,7},则(∁UA)∩B=( )
| A. | {4} | B. | {3,4,7} | C. | {3,7} | D. | ∅ |
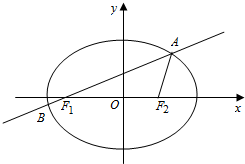 如图,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{2}}}{2}$,F1、F2为其左、右焦点,过F1的直线l交椭圆于A、B两点,△F1AF2的周长为$2(\sqrt{2}+1)$.
如图,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{2}}}{2}$,F1、F2为其左、右焦点,过F1的直线l交椭圆于A、B两点,△F1AF2的周长为$2(\sqrt{2}+1)$.