已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$.其焦距为2c.长轴长是焦距的$\sqrt{5}$倍.b.c的一个等比中项为$2\sqrt{2}$.则c=2．题目和参考答案——青夏教育精英家教网——

题目内容

17．已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$，其焦距为2c，长轴长是焦距的$\sqrt{5}$倍，b，c的一个等比中项为$2\sqrt{2}$，则c=2．

分析由题意可得2a=2$\sqrt{5}$c，bc=8，又a²-b²=c²，解方程可得c=2．

解答解：由长轴长是焦距的$\sqrt{5}$倍，b，c的一个等比中项为$2\sqrt{2}$，
可得2a=2$\sqrt{5}$c，bc=8，又a²-b²=c²，
解得a=2$\sqrt{5}$，b=4，c=2，
故答案为：2．

点评本题考查椭圆的方程和性质，同时考查等比数列的性质，考查运算能力，属于基础题．

练习册系列答案

仁爱英语同步阅读与完形填空周周练系列答案

拔尖特训系列答案

课课练与单元测试系列答案

世纪金榜小博士单元期末一卷通系列答案

单元测试AB卷台海出版社系列答案

黄冈新思维培优考王单元加期末卷系列答案

名校名师夺冠金卷系列答案

小学英语课时练系列答案

培优新帮手系列答案

天天向上一本好卷系列答案

相关题目

18．有一种鱼的身体吸收汞，汞的含量超过体重的1.00ppm（即百万分之一）时就会对人体产生危害．在30条鱼的样本中发现的汞含量是：
0.07 0.24 0.95 0.98 1.02 0.98 1.37 1.40 0.39 1.02
1.44 1.58 0.54 1.08 0.61 0.72 1.20 1.14 1.62 1.68
1.85 1.20 0.81 0.82 0.84 1.29 1.26 2.10 0.91 1.31
（1）用前两位数作为茎，画出样本数据的茎叶图；
（2）描述一下汞含量的分布特点；
（3）从实际情况看，许多鱼的汞含量超标在于有些鱼在出售之前没有被检查过，每批这种鱼的平均汞含量都比1.00ppm大吗？
（4）求出上述样本数据的平均数和标准差；
（5）有多少条鱼的汞含量在平局数与2倍标准差的和（差）的范围内？

如图，在四棱锥C-A₁ABB₁中，A₁A∥BB₁，A₁A⊥平面ABC，∠ACB=$\frac{π}{2}$，AC=AA₁=1，BC=BB₁=2．
（1）求证：平面A₁AC⊥平面B₁BC；
（2）若点C在棱AB上的射影为点P，求二面角A₁-PC-B₁的余弦值．

5．在△ABC中，角A，B，C所对的边分别为a，b，c，A=60°，b=2，S_△ABC=2$\sqrt{3}$，则a=2$\sqrt{3}$．

12．设S_n为数列{a_n}的前n项和，且对?n∈N^*，点（a_n，S_n）都在函数f（x）=-$\frac{1}{2}$x+$\frac{1}{2}$的图象上，等差数列{b_n}的首项b₁=1，公差d＞0，且b₂，b₅，b₁₄成等比数列．
（1）求数列{a_n}与{b_n}的通项公式
（2）若数列{c_n}对?n∈N^*，都有$\frac{{C}_{1}}{{a}_{1}}$+$\frac{{C}_{2}}{{a}_{2}}$+…+$\frac{{C}_{n}}{{a}_{n}}$=b_n+1成立，求数列{c_n•b_n}的前n项和T_n．

2．已知（$\sqrt{x}-\root{3}{x}$）ⁿ的展开式中所有项的二项式系数之和为1024．
（1）求展开式的所有有理数（指数为整数）；
（2）求（1-x）⁶+（1-x）⁷+…+（1-x）ⁿ展开式中x²项的系数．

9．设F为抛物线C：y²=4x的焦点，过F且倾斜角为45°的直线交C于A，B两点，则|AB|=（　　）

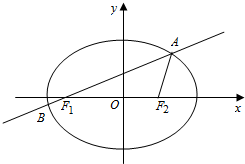如图，已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$的离心率为$\frac{{\sqrt{2}}}{2}$，F₁、F₂为其左、右焦点，过F₁的直线l交椭圆于A、B两点，△F₁AF₂的周长为$2（\sqrt{2}+1）$．
（1）求椭圆的标准方程；
（2）求△AOB面积的最大值（O为坐标原点）；
（3）直线m也过F₁与且与椭圆交于C、D两点，且l⊥m，设线段AB、CD的中点分别为M、N两点，试问：直线MN是否过定点？若是，求出定点坐标；若不是，请说明理由．

7．已知集合A={x|x²+y²=1}，B={y|y=cos²x}，则（　　）

A∩B={（0，1）}