题目内容
1.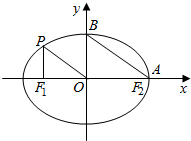 如图,从椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$上一点P向x轴作垂线,垂足恰为左焦点F1,又点A是椭圆与x 轴正半轴的交点,点B是椭圆与y轴正半轴的交点,且AB∥OP,则椭圆的离心率为( )
如图,从椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$上一点P向x轴作垂线,垂足恰为左焦点F1,又点A是椭圆与x 轴正半轴的交点,点B是椭圆与y轴正半轴的交点,且AB∥OP,则椭圆的离心率为( )| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
分析 由椭圆方程,可得A,B,P的坐标,再由直线平行的条件:斜率相等,结合离心率公式,计算即可得到.
解答 解:由椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$,可得A(a,0),B(0,b),F1(-c,0),
设P(-c,y),则$\frac{{c}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1,解得y=±$\frac{{b}^{2}}{a}$,可取P(-c,$\frac{{b}^{2}}{a}$),
由AB∥OP,则kAB=kOP,
即为-$\frac{b}{a}$=-$\frac{{b}^{2}}{ac}$,
即为b=c,
则a=$\sqrt{{b}^{2}+{c}^{2}}$=$\sqrt{2}$c,
即有e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$.
故选C.
点评 本题主要考查椭圆的离心率的求法,同时考查直线平行的条件:斜率相等,考查运算能力,属于中档题.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案
相关题目
9.设F为抛物线C:y2=4x的焦点,过F且倾斜角为45°的直线交C于A,B两点,则|AB|=( )
| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
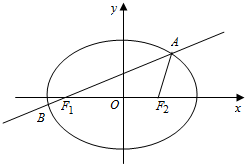 如图,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{2}}}{2}$,F1、F2为其左、右焦点,过F1的直线l交椭圆于A、B两点,△F1AF2的周长为$2(\sqrt{2}+1)$.
如图,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{{\sqrt{2}}}{2}$,F1、F2为其左、右焦点,过F1的直线l交椭圆于A、B两点,△F1AF2的周长为$2(\sqrt{2}+1)$.